
6.在锐角△ABC中,边长a=1,b=2,则边长c的取值范围是_______.
练习简答:1-4.BBCB; 1.在△ABC中,A>30° 0<sinA<1sinA>
0<sinA<1sinA>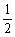 ;sinA>
;sinA>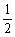
 30°<A<150°
30°<A<150° A>30°答案:B
A>30°答案:B
5.(2004春上海)在 中,
中, 分别是
分别是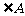 、
、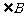 、
、 所对的边。若
所对的边。若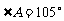 ,
,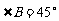 ,
,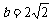 , 则
, 则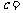 __________
__________
4.(2006全国Ⅰ)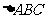 的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且
的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且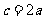 ,则
,则 ( )
( )
A. 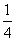 B.
B. 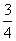 C.
C. 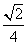 D.
D. 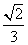
[填空题]
3..下列条件中,△ABC是锐角三角形的是 ( )
A.sinA+cosA= B.
B. ·
·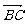 >0
>0
C.tanA+tanB+tanC>0 D.b=3,c=3 ,B=30°
,B=30°
2.(2004全国Ⅳ)△ABC中,a、b、c分别为∠A、∠B、∠C的对边,如果a、b、c成等差数列,∠B=30°,△ABC的面积为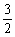 ,那么b等于
( )
,那么b等于
( )
A.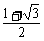 B.1+
B.1+
C. D.2+
D.2+
1.(2004浙江)在△ABC中,“A>30°”是“sinA>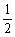 ”的
( )
”的
( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
4.边角互化是解三角形的重要手段.
同步练习 4.6 正弦、余弦定理 解斜三角形
[选择题]
2.利用正弦定理,可以解决以下两类问题:
(1)已知两角和任一边,求其他两边和一角;
(2)已知两边和其中一边的对角,求另一边的对角(从而进一步求出其他的边和角);3.利用余弦定理,可以解决以下两类问题:
(1) 已知三边,求三角;(2)已知两边和它们的夹角,求第三边和其他两角。
1.掌握三角形中的的基本公式和正余弦定理;
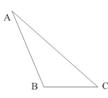
 [例1](2006天津)如图,在
[例1](2006天津)如图,在 中,
中,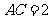 ,
,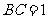 ,
, .
.
(1)求 的值;
的值;
(2)求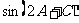 的值.
的值.
解(Ⅰ): 由余弦定理,

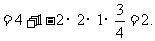
∴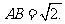
(Ⅱ)解:由 ,且
,且 得
得
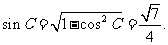
由正弦定理: 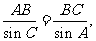
解得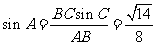 。所以,
。所以,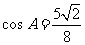 。由倍角公式
。由倍角公式
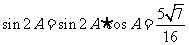 ,
,
且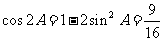 ,故
,故
 .
.
◆提炼方法:已知两边夹角,用余弦定理,由三角函数值求三角函数值时要注意“三角形内角”的限制.
[例2]在ΔABC中,已知a=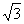 ,b=
,b=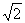 ,B=45°,求A,C及边c.
,B=45°,求A,C及边c.
解:由正弦定理得:sinA= ,因为B=45°<90°且b<a,
,因为B=45°<90°且b<a,
所以有两解A=60°或A=120°
(1)当A=60°时,C=180°-(A+B)=75°, c=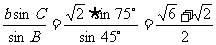 ,
,
(2)当A=120°时,C=180°-(A+B)=15 °,c=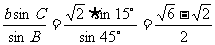
◆提炼方法:已知两边和其中一边的对角解三角形问题,用正弦定理求解,必需注意解的情况的讨论.
[例3](2006上海)如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救 甲船立即前往救援,同时把消息告知在甲船的南偏西30
甲船立即前往救援,同时把消息告知在甲船的南偏西30 ,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到
,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到 )?
)?
[解] 连接BC,由余弦定理得
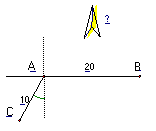 BC2=202+102-2×20×10COS120°=700
BC2=202+102-2×20×10COS120°=700
于是,BC=10

|
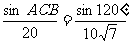 ,
∴sin∠ACB=
,
∴sin∠ACB=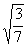 ,
,
∵∠ACB<90° ∴∠ACB=41°
∴乙船应朝北偏东71°方向沿直线前往B处救援
思路点拨:把实际问题转化为解斜三角形问题,在问题中构造出三角形,标出已知量、未知量,确定解三角形的方法;

[例4]已知⊙O的半径为R,,在它的内接三角形ABC中,有
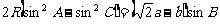 成立,求△ABC面积S的最大值.
成立,求△ABC面积S的最大值.
解:由已知条件得
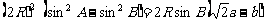 .即有
.即有 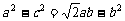 ,
,
又  ∴
∴ 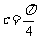 .
.
∴ 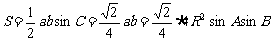
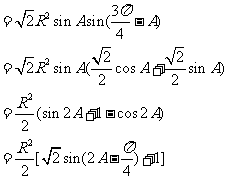
当 时,
时, 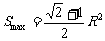 .
.
◆思路方法:1.边角互化是解三角形问题常用的手段.一般有两种思路:一是边化角;二是角化边。
2.三角形中的三角变换,应灵活运用正、余弦定理.在求值时,要利用三角函数的有关性质.
[研讨.欣赏]
(2006江西)如图,已知△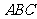 是边长为
是边长为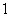 的正三角形,
的正三角形, 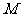 、
、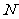 分别是边
分别是边 、
、 上的点,线段
上的点,线段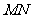 经过△
经过△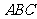 的中心
的中心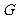 .设
.设 .
.
(1) 试将△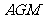 、△
、△ 的面积(分别记为
的面积(分别记为 与
与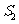 )表示为
)表示为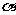 的函数;
的函数;
(2)  求
求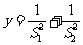 的最大值与最小值.
的最大值与最小值.
解:
(1)因为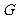 为边长为
为边长为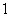 的正三角形
的正三角形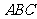 的中心,
的中心,
所以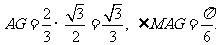
由正弦定理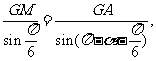
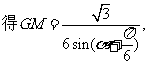

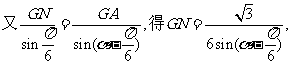
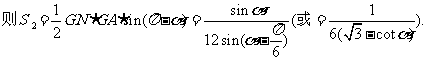
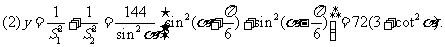
因为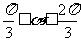 ,所以当
,所以当 时,
时,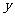 的最大值
的最大值 ;
;
当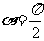 时,
时, 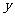 的最小值
的最小值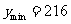 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com