
3.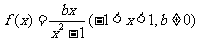 .
.
分析:利用导数可以研究函数的单调性,一般应先确定函数的定义域,再求导数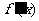 ,通过判断函数定义域被导数为零的点所划分的各区间内
,通过判断函数定义域被导数为零的点所划分的各区间内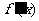 的符号,来确定函数
的符号,来确定函数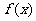 在该区间上的单调性.当给定函数含有字母参数时,分类讨论难于避免,不同的化归方法和运算程序往往使分类方法不同,应注意分类讨论的准确性.
在该区间上的单调性.当给定函数含有字母参数时,分类讨论难于避免,不同的化归方法和运算程序往往使分类方法不同,应注意分类讨论的准确性.
解: 1.函数定义域为R.
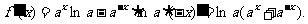
当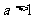 时,
时,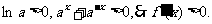
∴函数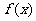 在
在 上是增函数.
上是增函数.
当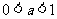 时,
时,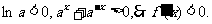
∴函数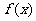 在
在 上是减函数.
上是减函数.
2. (
(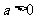 且
且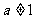 );
);
1.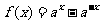 (
(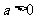 且
且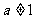 );
);
22.已知定义域为R的函数f(x)满足 .
.
(Ⅰ)若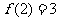 ,求
,求 ;又若
;又若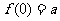 ,求
,求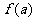 ;
;
(Ⅱ)设有且仅有一个实数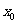 ,使得
,使得 ,求函数
,求函数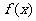 的解析表达式.
的解析表达式.
21.设函数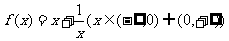 的图象为
的图象为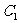 、
、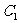 关于点A(2,1)的对称的图象为
关于点A(2,1)的对称的图象为 ,
, 对应的函数为
对应的函数为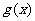 ,
,
(Ⅰ)求函数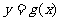 的解析式,并确定其定义域;
的解析式,并确定其定义域;
(Ⅱ)若直线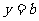 与
与 只有一个交点,求
只有一个交点,求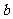 的值,并求出交点的坐标.
的值,并求出交点的坐标.
20.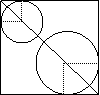 如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数,求函数
如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数,求函数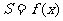 的解析式及
的解析式及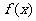 的值域.
的值域.
19.已知函数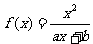 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3, x2=4.(1)求函数f(x)的解析式;
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3, x2=4.(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;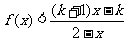 .
.
18.二次函数f(x)满足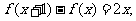 且f(0)=1.
且f(0)=1.
(1) 求f(x)的解析式;
(2) 在区间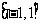 上,y= f(x)的图象恒在
上,y= f(x)的图象恒在 的图象上方,试确定实数m的范围.
的图象上方,试确定实数m的范围.
17.判断 在(-
在(- )上的单调性,并用定义证明。
)上的单调性,并用定义证明。
16.关于反函数给出下述命题:
①若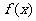 为奇函数,则
为奇函数,则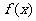 一定有反函数.
一定有反函数.
②函数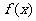 有反函数的充要条件是
有反函数的充要条件是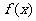 是单调函数.
是单调函数.
③若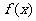 的反函数是
的反函数是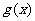 ,则函数
,则函数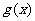 一定有反函数,且它的反函数是
一定有反函数,且它的反函数是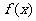
④设函数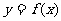 的反函数为
的反函数为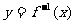 ,若点P(a,b)在
,若点P(a,b)在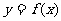 的图象上,
的图象上,
则点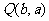 一定在
一定在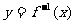 的图象上.
的图象上.
⑤若两个函数的图象关于直线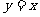 对称,则这两个函数一定互为反函数.
对称,则这两个函数一定互为反函数.
其中错误的命题是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com