
24.(山东理科16)函数y=loga(x+3)-1(a>0,a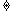 1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中mn>0,则
1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中mn>0,则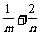 的最小值为
.
的最小值为
.
23.(山东理科2).已知集合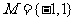 ,
, 则
则 (B)
(B)
(A) 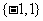 (B)
(B)  (C)
(C)
 (D)
(D)
22.(江西理科17).(本小题满分12分)
已知函数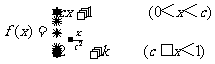 在区间(0,1)内连续,且
在区间(0,1)内连续,且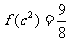 .
.
(1)求实数k和c的值;
(2)解不等式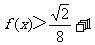
21.(重庆理科13)若函数f(x) = 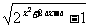 的定义域为R,则a的取值范围为_______.
的定义域为R,则a的取值范围为_______.
20.(重庆理科2)命题“若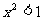 ,则
,则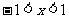 ”的逆否命题是( )
”的逆否命题是( )
A.若 ,则
,则 或
或 B.若
B.若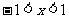 ,则
,则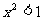
C.若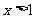 或
或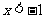 ,则
,则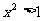 D.若
D.若 或
或 ,则
,则
19.(福建理科13)已知实数x、y满足 ,则
,则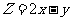 的取值范围是___
的取值范围是___ _______;
_______;
18.(福建理科7)已知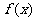 为R上的减函数,则满足
为R上的减函数,则满足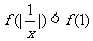 的实数
的实数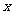 的取值范围是(C)
的取值范围是(C)
A.(-1,1) B.(0,1)
C.(-1,0)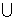 (0,1) D.(-
(0,1) D.(- ,-1)
,-1)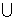 (1,+
(1,+ )
)
17.(福建理科3)已知集合A=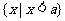 ,B=
,B= ,且
,且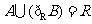 ,则实数
,则实数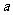 的取值范围是(C)
的取值范围是(C)
A.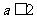 B. a<1 C.
B. a<1 C.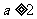 D.a>2
D.a>2
14.(湖北理科21)(本小题满分14分)
已知m,n为正整数.
(Ⅰ)用数学归纳法证明:当x>-1时,(1+x)m≥1+mx;
(Ⅱ)对于n≥6,已知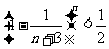 ,求证
,求证 ,m=1,1,2…,n;
,m=1,1,2…,n;
(Ⅲ)求出满足等式3n+4m+…+(n+2)m=(n+3)n的所有正整数n.
解:(Ⅰ)证:当x=0或m=1时,原不等式中等号显然成立,下用数学归纳法证明:
当x>-1,且x≠0时,m≥2,(1+x)m>1+mx. 1
(i)当m=2时,左边=1+2x+x2,右边=1+2x,因为x≠0,所以x2>0,即左边>右边,不等式①成立;
(ii)假设当m=k(k≥2)时,不等式①成立,即(1+x)k>1+kx,则当m=k+1时,因为x>-1,所以1+x>0.又因为x≠0,k≥2,所以kx2>0.
于是在不等式(1+x)k>1+kx两边同乘以1+x得
(1+x)k·(1+x)>(1+kx)(1+x)=1+(k+1)x+kx2>1+(k+1)x,
所以(1+x)k+1>1+(k+1)x,即当m=k+1时,不等式①也成立.
综上所述,所证不等式成立.
(Ⅱ)证:当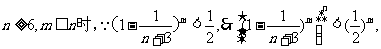
而由(Ⅰ),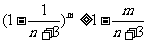

(Ⅲ)解:假设存在正整数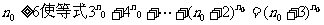 成立,
成立,
即有(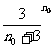 )+
)+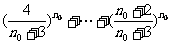 =1. ②
=1. ②
又由(Ⅱ)可得
(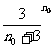 )+
)+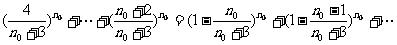
+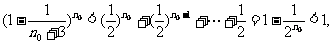 与②式矛盾,
与②式矛盾,
故当n≥6时,不存在满足该等式的正整数n.
故只需要讨论n=1,2,3,4,5的情形;
当n=1时,3≠4,等式不成立;
当n=2时,32+42=52,等式成立;
当n=3时,33+43+53=63,等式成立;
当n=4时,34+44+54+64为偶数,而74为奇数,故34+44+54+64≠74,等式不成立;
当n=5时,同n=4的情形可分析出,等式不成立.
综上,所求的n只有n=2,3.
15(湖南理科2).不等式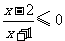 的解集是( D
)
的解集是( D
)
A.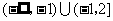 B.
B. C.
C. D.
D.
16(湖南理科14).设集合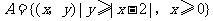 ,
,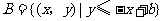 ,
,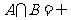 ,
,
(1) 的取值范围是 ;
的取值范围是 ;
(2)若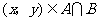 ,且
,且 的最大值为9,则
的最大值为9,则 的值是
.
的值是
.
(1) (2)
(2)
13.(湖北理科3)3.设P和Q是两个集合,定义集合P-Q=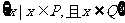 ,如果P={x|log2x<1},Q={x||x-2|<1},那么P-Q等于(B)
,如果P={x|log2x<1},Q={x||x-2|<1},那么P-Q等于(B)
A.{x|0<x<1} B.{x|0<x≤1} C.{x|1≤x<2} D.{x|2≤x<3}
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com