
12.(浙江理科17)设 为实数,若
为实数,若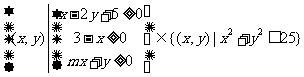 ,则
,则 的取值范围是_____________。
的取值范围是_____________。
11.(浙江理科13)不等式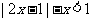 的解集是_____________。
的解集是_____________。
10.(浙江理科1)“ ”是“
”是“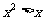 ”的
”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
7.(上海理科15)已知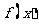 是定义域为正整数集的函数,对于定义域内任意的
是定义域为正整数集的函数,对于定义域内任意的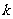 ,若
,若 成立,则
成立,则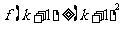 成立,下列命题成立的是(D)
成立,下列命题成立的是(D)
A、若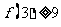 成立,则对于任意
成立,则对于任意 ,均有
,均有 成立
成立
B、若 成立,则对于任意的
成立,则对于任意的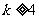 ,均有
,均有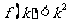 成立
成立
C、若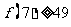 成立,则对于任意的
成立,则对于任意的 ,均有
,均有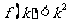 成立
成立
D、若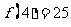 成立,则对于任意的
成立,则对于任意的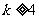 ,均有
,均有 成立
成立
8(天津理科2)设变量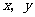 满足约束条件
满足约束条件 则目标函数
则目标函数 的最大值为( B )
的最大值为( B )
A.4 B.11 C.12 D.14
9(天津理科9)设 均为正数,且
均为正数,且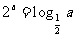 ,
,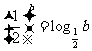 ,
, .则( A )
.则( A )
A.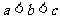 B.
B.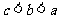 C.
C.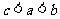 D.
D.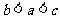
6.(上海理科13)已知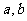 为非零实数,且
为非零实数,且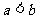 ,则下列命题成立的是(C)
,则下列命题成立的是(C)
A、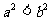 B、
B、 C、
C、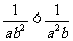 D、
D、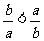
4.(北京理科12)已知集合 ,
,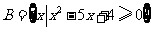 .若
.若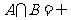 ,则实数
,则实数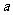 的取值范围是 (2,3) .
的取值范围是 (2,3) .
5(上海理科6)已知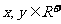 ,且
,且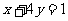 ,则
,则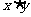 的最大值为
的最大值为
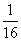
3.(北京理科7)如果正数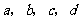 满足
满足 ,那么( A )
,那么( A )
A.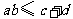 ,且等号成立时
,且等号成立时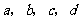 的取值唯一
的取值唯一
B.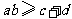 ,且等号成立时
,且等号成立时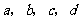 的取值唯一
的取值唯一
C.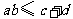 ,且等号成立时
,且等号成立时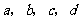 的取值不唯一
的取值不唯一
D.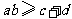 ,且等号成立时
,且等号成立时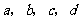 的取值不唯一
的取值不唯一
2.(北京理科6)若不等式组 表示的平面区域是一个三角形,则
表示的平面区域是一个三角形,则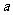 的取值范围是( D )
的取值范围是( D )
A. B.
B.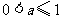 C.
C. D.
D.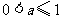 或
或
44.(全国Ⅱ)17.(本小题满分10分)
在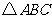 中,已知内角
中,已知内角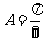 ,边
,边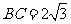 .设内角
.设内角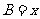 ,周长为
,周长为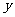 .
.
(1)求函数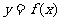 的解析式和定义域;
的解析式和定义域;
(2)求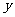 的最大值.
的最大值.
解:(1)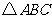 的内角和
的内角和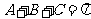 ,由
,由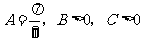 得
得 .
.
应用正弦定理,知
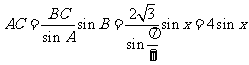 ,
,
 .
.
因为 ,
,
所以 ,
,
(2)因为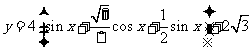
 ,
,
所以,当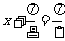 ,即
,即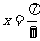 时,
时,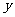 取得最大值
取得最大值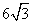 .
.
43.(全国Ⅰ文)(17)(本小题满分10分)
设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,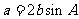 .
.
(Ⅰ)求B的大小;
(Ⅱ)若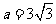 ,
,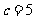 ,求b.
,求b.
解:(Ⅰ)由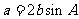 ,根据正弦定理得
,根据正弦定理得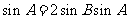 ,所以
,所以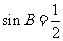 ,
,
由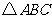 为锐角三角形得
为锐角三角形得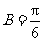 .
.
(Ⅱ)根据余弦定理,得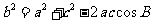

 .
.
所以,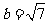 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com