
7. (2006四川文、理)从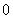 到
到 这
这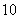 个数字中任取
个数字中任取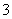 个数字组成一个没有重复数字的三位数,这个数不能被
个数字组成一个没有重复数字的三位数,这个数不能被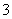 整除的概率为( )
整除的概率为( )
(A)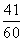 (B)
(B)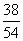 (C)
(C)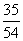 (D)
(D)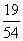
6.(2006福建理)在一个口袋中装有5个白球和3个黑球,这些球除颜色外完全相同,从中摸出3个球,至少摸到2个黑球的概率等于( )
A.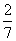 B.
B.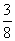 C.
C.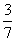 D.
D.
5.(2007重庆文、理)从5张100元,3张200元,2张300元的奥运预赛门票中任取3张,则所取3张中至少有2张价格相同的概率为( )
(A)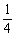 (B)
(B) (C)
(C)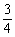 (D)
(D)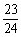
4. (2008重庆理)已知随机变量 服从正态分布N(3,a2),则P (
服从正态分布N(3,a2),则P ( <3) =( )
<3) =( )
(A) (B)
(B)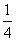 (C)
(C)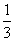 (D)
(D)
3. (2008山东理)在某地的奥运火炬传递活动中,有编号为1,2,3,…,18的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成3为公差的等差数列的概率为( )
(A)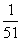 (B)
(B)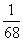 (C)
(C)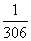 (D)
(D)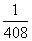
2.(2008辽宁文、理) 4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( )
A.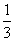 B.
B. C.
C.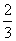 D.
D.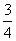
1.(2008福建文)某一批花生种子,如果每一粒发芽的概率为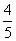 ,那么播下3粒种子恰有2粒发芽的概率是( )
,那么播下3粒种子恰有2粒发芽的概率是( )
A.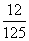 B.
B. C.
C. D.
D.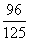
20.解:设事件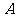 为“方程
为“方程 有实根”.
有实根”.
当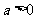 ,
,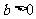 时,方程
时,方程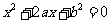 有实根的充要条件为
有实根的充要条件为 .
.
(Ⅰ)基本事件共12个:
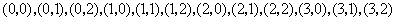 .其中第一个数表示
.其中第一个数表示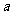 的取值,第二个数表示
的取值,第二个数表示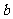 的取值.
的取值.
事件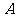 中包含9个基本事件,事件
中包含9个基本事件,事件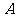 发生的概率为
发生的概率为 .
.
(Ⅱ)试验的全部结束所构成的区域为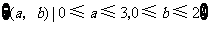 .
.
构成事件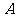 的区域为
的区域为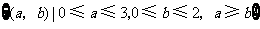 .
.
所以所求的概率为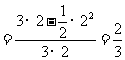 .
.
19.解:设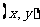 表示一个基本事件,则掷两次骰子包括:
表示一个基本事件,则掷两次骰子包括: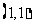 ,
, ,
,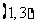 ,
,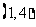 ,
, ,
,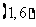 ,
,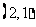 ,
,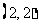 ,……,
,……,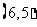 ,
,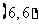 ,共36个基本事件.
,共36个基本事件.
(1)用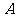 表示事件“
表示事件“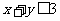 ”,则
”,则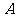 的结果有
的结果有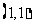 ,
, ,
,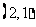 ,共3个基本事件.
,共3个基本事件.
∴ .
.
答:事件“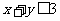 ”的概率为
”的概率为 .
.
(2)用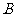 表示事件“
表示事件“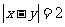 ”,
”,
则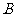 的结果有
的结果有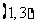 ,
,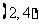 ,
, ,
, ,
, ,
, ,
, ,
,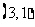 ,共8个基本事件. ∴
,共8个基本事件. ∴ .
.
答:事件“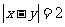 ”的概率为
”的概率为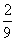 .
.
18.解:(Ⅰ)从8人中选出日语、俄语和韩语志愿者各1名,其一切可能的结果组成的基本事件空间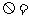 {
{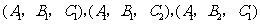 ,
, ,
,
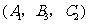 ,
,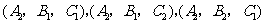 ,
,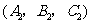 ,
,
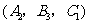 ,
, ,
, ,
,
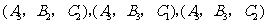 }
}
由18个基本事件组成.由于每一个基本事件被抽取的机会均等,因此这些基本事件的发生是等可能的.
用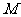 表示“
表示“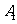 恰被选中”这一事件,则
恰被选中”这一事件,则 {
{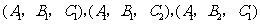 ,
,
 },事件
},事件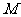 由6个基本事件组成,
由6个基本事件组成,
因而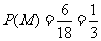 .
.
(Ⅱ)用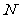 表示“
表示“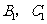 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件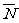 表示“
表示“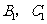 全被选中”这一事件,由于
全被选中”这一事件,由于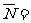 {
{ },事件
},事件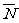 有3个基本事件组成,
有3个基本事件组成,
所以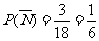 ,由对立事件的概率公式得
,由对立事件的概率公式得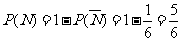 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com