
4.(2007韶关一模文)有3张奖券,其中2张可中奖,现3个人按顺序依次从中抽一张,小明最后抽,
则他抽到中奖券的概率是( )
(A)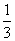 (B)
(B)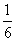 (C)
(C)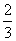 (D)
(D)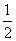
3.( 2005年广东)先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有1,2,3,4,5,6),
骰子朝上的面的点数分别为x,y,则使 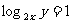 的概率为( )
的概率为( )
A.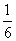 B.
B.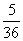 C.
C.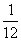 D.
D.
2.(2008惠州调研二理)方程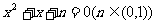 有实根的概率为(
).
有实根的概率为(
).
A、 B、
B、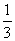 C、
C、 D、
D、
1.(2008辽宁文、理) 4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( )
A.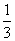 B.
B.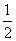 C.
C.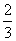 D.
D.
20.(2006陕西理)如图,三定点A(2,1),B(0,-1),C(-2,1); 三 动点D,E,M满足=t, = t ,
=t , t∈[0,1]. (Ⅰ) 求动直线DE斜率的变化范围; (Ⅱ)求动点M的轨迹方程.

历届高考中的“平面向量”试题精选(自我测试)
19、(2002全国新课程文、理,天津文、理)已知两点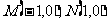 ,且点
,且点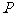 使
使 ,
,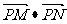 ,
, 成公差小于零的等差数列
成公差小于零的等差数列 (1)点P的轨迹是什么曲线?
(1)点P的轨迹是什么曲线?
(2)若点P坐标为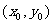 ,记
,记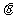 为
为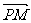 与
与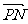 的夹角,求
的夹角,求 。
。
17.(2006湖北理)设函数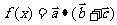 ,其中向量
,其中向量 ,
,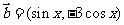
 ,
, 。 (Ⅰ)、求函数
。 (Ⅰ)、求函数 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅱ)将函数 的图像按向量
的图像按向量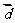 平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的
平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的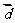 。
。
 18.(2004湖北文、理) 如图,在Rt△ABC中,已知BC=a.若长为2a的线段PQ以点A为中点,问
18.(2004湖北文、理) 如图,在Rt△ABC中,已知BC=a.若长为2a的线段PQ以点A为中点,问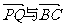 的夹 角θ取何值时
的夹 角θ取何值时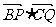 的值最大?并求出这个最大值.
的值最大?并求出这个最大值.
16.(2006全国Ⅱ卷理)已知向量a=(sinθ,1),b=(1,cosθ),-<θ<.
(Ⅰ)若a⊥b,求θ; (Ⅱ)求|a+b|的最大值.
15.(2007广东理)已知△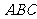 顶点的直角坐标分别为
顶点的直角坐标分别为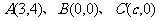 .
.
(1)若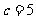 ,求sin∠
,求sin∠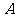 的值; (2)若∠
的值; (2)若∠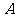 是钝角,求
是钝角,求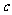 的取值范围.
的取值范围.
14、(2005江苏)在 中,O为中线AM上一个动点,若AM=2,则
中,O为中线AM上一个动点,若AM=2,则 的最小值是__________。
的最小值是__________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com