
3.
 算法案例:
算法案例:
⑴辗转相除法与更相减损法-----求两个正整数的最大公约数;
⑵秦九韶算法------求多项式的值;
⑶进位制----------各进制数之间的互化。
2.基本算法语句:





 ⑴输入语句: INPUT “提示内容”;变量 ;输出语句:PRINT “提示内容”;表达式
⑴输入语句: INPUT “提示内容”;变量 ;输出语句:PRINT “提示内容”;表达式




 赋值语句: 变量=表达式
赋值语句: 变量=表达式
 ⑵条件语句:①
②
⑵条件语句:①
②





 IF 条件 THEN
IF 条件 THEN
IF 条件 THEN
IF 条件 THEN
语句体 语句体1
END IF ELSE
 语句体2
语句体2
END IF

⑶循环语句:①当型: ②直到型:





 WHILE 条件
DO
WHILE 条件
DO
循环体 循环体
WEND LOOP UNTIL 条件
1.程序框图:
⑴图形符号:


 ①
终端框(起止况);②
输入、输出框;⑥ 连接点。
①
终端框(起止况);②
输入、输出框;⑥ 连接点。
 ③
③

 处理框(执行框);④
判断框;⑤ 流程线
;
处理框(执行框);④
判断框;⑤ 流程线
;
⑵程序框图分类:


 ①顺序结构:
②条件结构:
③循环结构:
①顺序结构:
②条件结构:
③循环结构:





 r=0? 否
求n除以i的余数
r=0? 否
求n除以i的余数

 输入n
是
输入n
是





 n不是质素 n是质数
i=i+1
n不是质素 n是质数
i=i+1







 i=2
i=2


 i
i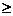 n或r=0?否
n或r=0?否
 是
是
注:循环结构分为:Ⅰ.当型(while型)--先判断条件,再执行循环体;
Ⅱ.直到型(until型)--先执行一次循环体,再判断条件。
5.独立性检验(分类变量关系):
随机变量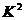 越大,说明两个分类变量,关系越强,反之,越弱。
越大,说明两个分类变量,关系越强,反之,越弱。
4.回归分析中回归效果的判定:
⑴总偏差平方和: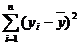 ⑵残差:
⑵残差: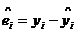 ;⑶残差平方和:
;⑶残差平方和: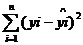 ;⑷回归平方和:
;⑷回归平方和: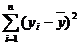 -
-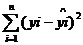 ;⑸相关指数
;⑸相关指数 。
。
注:① 得知越大,说明残差平方和越小,则模型拟合效果越好;
得知越大,说明残差平方和越小,则模型拟合效果越好;
② 越接近于1,,则回归效果越好。
越接近于1,,则回归效果越好。
3.相关系数(判定两个变量线性相关性):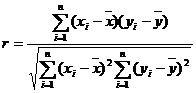
注:⑴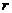 >0时,变量
>0时,变量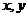 正相关;
正相关;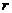 <0时,变量
<0时,变量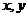 负相关;
负相关;
⑵①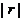 越接近于1,两个变量的线性相关性越强;②
越接近于1,两个变量的线性相关性越强;②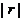 接近于0时,两个变量之间几乎不存在线性相关关系。
接近于0时,两个变量之间几乎不存在线性相关关系。
2.总体特征数的估计:
⑴样本平均数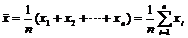 ;
;
⑵样本方差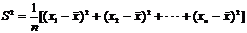
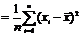 ;
;
⑶样本标准差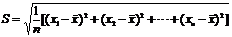 =
=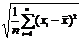 ;
;
1.抽样方法
⑴简单随机抽样:一般地,设一个总体的个数为N,通过逐个不放回的方法从中抽取一个容量为n的样本,且每个个体被抽到的机会相等,就称这种抽样为简单随机抽样。
注:①每个个体被抽到的概率为 ;
;
②常用的简单随机抽样方法有:抽签法;随机数法。
⑵系统抽样:当总体个数较多时,可将总体均衡的分成几个部分,然后按照预先制定的
规则,从每一个部分抽取一个个体,得到所需样本,这种抽样方法叫系统抽样。
注:步骤:①编号;②分段;③在第一段采用简单随机抽样方法确定其时个体编号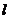 ;
;
④按预先制定的规则抽取样本。
⑶分层抽样:当已知总体有差异比较明显的几部分组成时,为使样本更充分的反映总体的情况,将总体分成几部分,然后按照各部分占总体的比例进行抽样,这种抽样叫分层抽样。
注:每个部分所抽取的样本个体数=该部分个体数

2.概率公式:
⑴互斥事件(有一个发生)概率公式:P(A+B)=P(A)+P(B);
⑵古典概型: ;
;
⑶几何概型: ;
;
1.事件的关系:
⑴事件B包含事件A:事件A发生,事件B一定发生,记作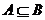 ;
;
⑵事件A与事件B相等:若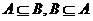 ,则事件A与B相等,记作A=B;
,则事件A与B相等,记作A=B;
⑶并(和)事件:某事件发生,当且仅当事件A发生或B发生,记作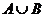 (或
(或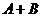 );
);
⑷并(积)事件:某事件发生,当且仅当事件A发生且B发生,记作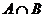 (或
(或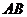 ) ;
) ;
⑸事件A与事件B互斥:若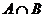 为不可能事件(
为不可能事件(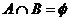 ),则事件A与互斥;
),则事件A与互斥;
﹙6﹚对立事件: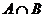 为不可能事件,
为不可能事件,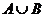 为必然事件,则A与B互为对立事件。
为必然事件,则A与B互为对立事件。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com