22.解:(1) 由f(x)＝知x满足: x²+ ≥0, ∴　 ≥0 , ∴≥0

∴ ≥0, 故x＞0, 或x≤－1.f(x)定义域为: (－∞, －1]∪(0,+∞)

(2)∵ a_n+1²＝a_n²+ , 则a_n+1²－a_n² ＝ 于是有: ＝ a_n+1²－a₁² ＝ a_n+1²－1

要证明:

只需证明: 　( *) 下面使用数学归纳法证明: (n≥1,n∈N*)　 ①在n＝1时, a₁＝1, ＜a₁＜2, 则n＝1时 (* )式成立.

②假设n＝k时, 　成立, 由

要证明: 　只需2k+1≤ 只需(2k+1)³≤8k(k+1)²

只需证: 　, 只需证: 4k²+11k+8＞0, 而4k²+11k+8＞0在k≥1时恒成立.　 于是: . 因此 得证. 综合①②可知( *)式得证, 从而原不等式成立.

(3)要证明: 　,由(2)可知只需证: 　(n≥2)　 (** )

下面用分析法证明: (**)式成立. 要使(**)成立,只需证: (3n－2)＞(3n－1)

即只需证: (3n－2)³n＞(3n－1)³(n－1), 只需证:2n＞1. 而2n＞1在n≥1时显然成立,故(**)式得证.于是由(**)式可知有: + +…+≤ 因此有: S_n＝a₁+a₂+…+a_n≤1+2(+ +…+) ＝

21.解：(I)设该同学连对线的个数为y，得分为ξ,则y=0，1，2，4

　　　　　 ∴ξ=0，2，4，8

　则ξ的分布列为

ξ	0	2	4	8
P

(II)Eξ=0×+2×+4×+8×=2, 答：该人得分的期望为2分

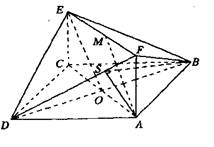
20.(1)解：记AC与BD的交点为O，连接OE

∵O，M分别是AC、EF的中点，且四边形ACEF是矩形，∴四边形AOEM是平行四边形，

∴AM//OE， 　 又OE平面BDE，AM平面BDE，∴AM//平面BDE

　 (2)在平面AFD中过A作AS⊥DF，垂足为S，连接BS，

∵AB⊥AF，AB⊥AD，ADAF=A，∴AB⊥平面ADF.

又DF平面ADF，∴DF⊥AB，又DF⊥AS，ABAS=A，

∴DF⊥平面ABS.又BS平面ABS，∴DF⊥SB.

∴∠BSA是二面角A-DF-B的平面角.

在Rt△ASB中，AS

∴　　 ∴∠ASB=60°

22、已知点(a_n,a_n－1)在曲线f(x)＝上, 且a₁＝1.(1)求f(x)的定义域;

(2)求证: (n∈N*)

(3)求证: 数列{a_n}前n项和 (n≥1, n∈N*)

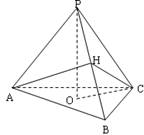15 方法一：观察正三棱锥P–ABC，O为底面中心，不妨将底面正△ABC固定，顶点P运动，相邻两侧面所成二面角为∠AHC．当PO→0时，面PAB→△OAB，面PBC→△OBC，∠AHC→π,当PO→+∞时，∠AHC→∠ABC=.故<∠AHC <π，选A．

方法二：不妨设AB=2，PC= x，则x > OC =.等腰△PBC中，S_△PBC =x·CH =·2·CH =,等腰△AHC中，sin.由x>得<1，∴＜∠AHC＜π.

19解：(1)甲经过到达N，可分为两步：第一步：甲从M经过的方法数：种；第二步：甲从到N的方法数：种；所以：甲经过的方法数为；

　　　 所以：甲经过的概率

　(2)由(1)知：甲经过的方法数为：；乙经过的方法数也为：；所以甲、乙两人相遇经点的方法数为： ＝81； 甲、乙两人相遇经点的概率

　(3)甲、乙两人沿最短路径行走，只可能在、、、处相遇，他们在相遇的走法有种方法；所以：＝164

甲、乙两人相遇的概率

21.在一次语文测试中，有一道我国四大文学名著《水浒传》、《三国演义》、《西游记》、《红楼梦》与它们的作者的连线题，连对一个得2分，连错一个不得分.(Ⅰ)求该同学得分的分布列；(Ⅱ)求该同学得分的数学期望.

20、已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB=，AF=1，M是线段EF的中点.(1)求证：AM//平面BDE；　 (2)求二面角A-DF-B的大小.

19、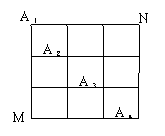如图，在某城市中，M，N两地之间有整齐的方格形道路网，、、、是道路网中位于一条对角线上的4个交汇处，今在道路网M、N处的甲、乙两人分别要到M，N处，他们分别随机地选择一条沿街的最短路径，同时以每10分钟一格的速度分别向N，M处行走，直到到达N，M为止。(1)求甲经过的概率；

(2)求甲、乙两人相遇经点的概率；(3)求甲、乙两人相遇的概率；

18．的值为　　　　　　　　

17.已知数列{}的通项公式为，则+++= 　　　　

16. 设1+(1+x)²+(1+2x)²+(1+3x)²+…+(1+nx)²=a₀+a₁x+a₂x²，则的值是CA．0　 B．　　 C．1　 D．2