
粒子由P运动到Q
的时间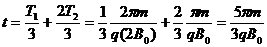
l = 2(R2sin60°-R1sin60°)=2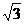 h
h
由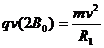 得
得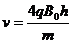
(2)根据运动的对称性,PQ的距离为
由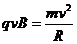 和B1=2B2可知R2=2R1=4h
和B1=2B2可知R2=2R1=4h
 14.如图,在广阔的宇宙空间存在这样一个远离其他空间的区域,以MN为界,上部分的匀强磁场的磁感应强度为B1,下部分的匀强磁场的磁感应强度为B2,B1=B0=2B2,方向相同,且磁场区域足够大.在距离界线为h的P点有一宇航员处于静止状态,宇航员以平行于界线的速度抛出一质量为m、带电量-q的球,发现球在界线处速度方向与界线成60°角进入下部分磁场,然后当宇航员沿与界线平行的直线匀速到达目标Q点时,刚好又接住球而静止.求:
14.如图,在广阔的宇宙空间存在这样一个远离其他空间的区域,以MN为界,上部分的匀强磁场的磁感应强度为B1,下部分的匀强磁场的磁感应强度为B2,B1=B0=2B2,方向相同,且磁场区域足够大.在距离界线为h的P点有一宇航员处于静止状态,宇航员以平行于界线的速度抛出一质量为m、带电量-q的球,发现球在界线处速度方向与界线成60°角进入下部分磁场,然后当宇航员沿与界线平行的直线匀速到达目标Q点时,刚好又接住球而静止.求:
(1)小球在两磁场中运动的轨道半径大小(仅用h表示)和小球的速度;
(2)宇航员的质量(用已知量表示)
[解析](1)画出小球在磁场B1中运动的轨迹如图所示,可知R1-h=R1cos60°,R1=2h
 [思路点拨]利用法拉第电磁感应定律及欧姆定律得到
[思路点拨]利用法拉第电磁感应定律及欧姆定律得到 ,该关系式在第(2)及第(3)小题的讨论中与动量定理相结合均能顺利解决问题.必须明确的是求解电量时往往利用电流平均值概念.
,该关系式在第(2)及第(3)小题的讨论中与动量定理相结合均能顺利解决问题.必须明确的是求解电量时往往利用电流平均值概念.
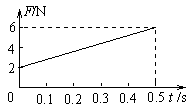
拉力作用时间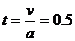 s,此时Fmax=6N;
s,此时Fmax=6N;
t = 0时,F=ma=2N
(4)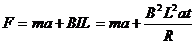 ,
,
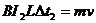 ,即
,即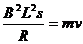 ,
,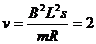 m/s
所以
m/s
所以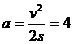 m/s2
m/s2
(3)拉力撤去时,导体杆的速度为v,拉力撤去后杆运动时间为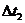 ,平均感应电流为I2,根据动量定理有:
,平均感应电流为I2,根据动量定理有:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com