1.(★★★★)等比数列{a_n}的首项a₁=－1,前n项和为S_n,若，则S_n等于(    )

8.(★★★★★)已知函数f(x)在(－∞,0)∪(0,+∞)上有定义，且在(0,+∞)上是增函数，f(1)=0,又g(θ)=sin²θ－mcosθ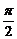－2m,θ∈［0,］,设M={m|g(θ)<0,m∈R},N={m|f［g(θ)］<0},求M∩N.

［学法指导］怎样学好函数

学习函数要重点解决好四个问题：准确深刻地理解函数的有关概念；揭示并认识函数与其他数学知识的内在联系；把握数形结合的特征和方法；认识函数思想的实质，强化应用意识.

(一)准确、深刻理解函数的有关概念

概念是数学的基础，而函数是数学中最主要的概念之一，函数概念贯穿在中学代数的始终.数、式、方程、函数、排列组合、数列极限等是以函数为中心的代数.近十年来，高考试题中始终贯穿着函数及其性质这条主线.

(二)揭示并认识函数与其他数学知识的内在联系.函数是研究变量及相互联系的数学概念，是变量数学的基础，利用函数观点可以从较高的角度处理式、方程、不等式、数列、曲线与方程等内容.在利用函数和方程的思想进行思维中，动与静、变量与常量如此生动的辩证统一，函数思维实际上是辩证思维的一种特殊表现形式.

所谓函数观点，实质是将问题放到动态背景上去加以考虑.高考试题涉及5个方面：(1)原始意义上的函数问题；(2)方程、不等式作为函数性质解决；(3)数列作为特殊的函数成为高考热点；(4)辅助函数法；(5)集合与映射，作为基本语言和工具出现在试题中.

(三)把握数形结合的特征和方法

函数图象的几何特征与函数性质的数量特征紧密结合，有效地揭示了各类函数和定义域、值域、单调性、奇偶性、周期性等基本属性，体现了数形结合的特征与方法，为此，既要从定形、定性、定理、定位各方面精确地观察图形、绘制图形，又要熟练地掌握函数图象的平移变换、对称变换.

(四)认识函数思想的实质，强化应用意识

函数思想的实质就是用联系与变化的观点提出数学对象，抽象数量特征，建立函数关系，求得问题的解决.纵观近几年高考题，考查函数思想方法尤其是应用题力度加大，因此一定要认识函数思想实质，强化应用意识.

(1)写出总造价y(元)与污水处理池长x(米)的函数关系式，并指出其定义域.

(2)求污水处理池的长和宽各为多少时，污水处理池的总造价最低？并求最低总造价.

7.(★★★★★)某工厂拟建一座平面图(如下图)为矩形且面积为200平方米的三级污水处理池，由于地形限制，长、宽都不能超过16米，如果池外周壁建造单价为每米400元，中间两条隔墙建造单价为每米248元，池底建造单价为每平方米80元(池壁厚度忽略不计，且池无盖).

求证：.

6.(★★★★★)定义在(－1，1)上的函数f(x)满足①对任意x、y∈(－1,1),都有f(x)+f(y)=f();②当x∈(－1,0)时，有f(x)>0.

(3)解不等式f［x(x－)］<.

5.(★★★★★)设f(x)=.

(1)证明：f(x)在其定义域上的单调性；

(2)证明：方程f^-1(x)=0有惟一解；

4.(★★★★)设a为实数，函数f(x)=x²+|x－a|+1,x∈R.

(1)讨论f(x)的奇偶性；

(2)求f(x)的最小值.

3.(★★★★)若关于x的方程2^2x+2^xa+a+1=0有实根，则实数a的取值范围是_________.