26. （10分）已知：如图，梯形ABCD中，AD∥BC，AB＝CD＝3cm，∠C＝60°，BD⊥CD．
⑴ 求BC、 AD的长度；
⑵ 若点P从点B开始沿BC边向点C以2cm／秒的速度运动，点Q从点C开始沿CD边向点D以1cm／秒的速度运动，当 P、Q分别从B、C同时出发时，写出五边形ABPQD的面积S与运动时间t之间的函数关系式，并写出自变量t的取值范围（不包含点P在B、C两点的情况）；
⑶ 在⑵的前提下，是否存在某一时刻t，使线段PQ把梯形ABCD分成两部分的面积比为1∶5？若存在，求出t的值；若不存在，请说明理由．

25. （10分）已知：如图，⊙O与⊙P相交于A、B两点，点 P在⊙O上，⊙O的弦AC切⊙P于点A，CP及其延长线交⊙P于D、E，过点 E作EF⊥CE交CB的延长线于F．
⑴ 求证：BC是⊙P的切线；
⑵ 若CD＝2，CB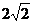＝，求EF的长；
⑶ 若设k＝PE：CE，是否存在实数k，使△PBD恰好是等边三角形？若存在，求出k的值；若不存在，请说明理由．

24.（8分）在抗击“非典”的斗争中，某市根据疫情的发展状况，决定全市中、小学放假两周，以切实保障广大中、小学生的安全．腾飞中学初三（1）班的全体同学在自主完成学习任务的同时，不忘关心同学们的安危，两周内全班每两个同学都通过一次电话，互相勉励，共同提高．如果该班有56名同学，那么同学们之间共通了多少次电话？
为解决该问题，我们可把该班人数n与通电话次数s间的关系用下列模型来表示：

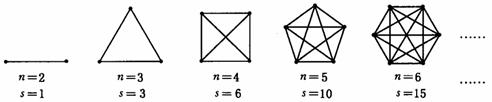
⑴ 若把n作为点的横坐标，s作为纵坐标，根据上述模型中的数据，在给出的平面直角坐标系中，描出相应各点，并用平滑的曲线连接起来；
⑵ 根据日中各点的排列规律，猜一猜上述各点会不会在某一函数的图像上？如果在，求出该函数的解析式；
⑶根据⑵中得出的函数关系式，求该班56名同学间共通了多少次电话．

23. （8分）某校餐厅计划购买12张餐桌和一批餐椅，现从甲、乙两商场了解到：同一型号的餐桌报价每张均为200元，餐椅报价每把均为50元．中商场称：每购买一张餐桌赠送一把餐椅；乙商场规定：所有餐桌椅均按报价的八五折销售．那么，什么情况下到甲商场购买更优惠？

22. （8分）如图，在矩形 ABCD中，F是BC边上一点，AF的延长线交DC的延长线于G，DE⊥AG于E，且DE＝DC．根据上述条件，请在图中找出一对全等三角形，并证明你的结论．

21. （6分）在争创全国卫生城市的活动中，我市一“青年突击队”决定义务清运一堆重达100吨的垃圾．开工后，附近居民主动参加到义务劳动中，使清运垃圾的速度比原计划提高了一倍，结果提前4小时完成任务，问“青年突击队”原计划每小时清运多少吨垃圾？

参考数据：
             sin66．8°≈ 0．9191     cos 66．8°≈ 0．393
             sin67．4°≈ 0．9231     cos 67．4°≈ 0．3846
             sin68．4°≈ 0．9298     cos 68．4°≈ 0．368l
             sin70．6°≈ 0．9432     cos70．6°≈ 0．3322