
 物线的解析式。
物线的解析式。
(4)在抛物线上取两点J、K,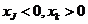 ,连结OJ、JK、OK,使得角OKJ=60°,再
,连结OJ、JK、OK,使得角OKJ=60°,再
以OK、OJ、JK分别作等边三角形OKL、OJM、OKN,请你求出经过M、N、L三点的抛
的面积为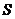 ,且
,且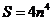 .
. 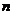 是不大于40的整数,求OP2的最小值.
是不大于40的整数,求OP2的最小值.
(3)F(m,n)(m>0)是抛物线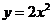 上的点,OF⊥FG,G(
上的点,OF⊥FG,G(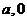 )(a>m). △O FG
)(a>m). △O FG
(2)存在一点D在劣弧AB上运动(不与A、B重合)设D( ,
,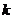 ),问抛物线上是否存在点E使得三角形ABD与三角形ABE的面积相等,若存在,求出点E,若不存在,请说明理由。
),问抛物线上是否存在点E使得三角形ABD与三角形ABE的面积相等,若存在,求出点E,若不存在,请说明理由。
友情提醒:C点的速度为
(1)当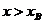 时,抛物线上存在一动点C,则随着C点的向上运动,三角形ABC面积不断增加,问三角形ABC面积每秒的增加量
时,抛物线上存在一动点C,则随着C点的向上运动,三角形ABC面积不断增加,问三角形ABC面积每秒的增加量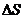 是什么?
是什么?
21.(本题满分13分)已知抛物线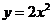 ,
,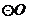 与抛物线交于A、B两点,AB两点所在的直线为
与抛物线交于A、B两点,AB两点所在的直线为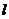 ,
,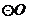 的半径为2。
的半径为2。
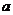 、
、 满足什么关系?
满足什么关系?
五、综合题(本大题共两小题,每小题各13分,总分26分,请在答题时应注意解答过程,证明以及演算的必要步骤)
(4)若不等式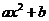 >
>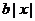 在实数范围内恒成立,则
在实数范围内恒成立,则
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com