29.（10分） 如图，在矩形ABCD中，AD=8,点E是AB边上的一点，AE=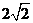,过D,E两点作直线PQ，与BC边所在的直线MN相交于点F。（1）求tan∠ADE的值；

（2）点G是线段AD上的一个动点（不运动至点A,D），GH⊥DE垂足为H，设DG为x，四边形AEHG的面积为y，请求出y与x之间的函数关系式；

⑵求快乐公司所购买的200件产品A的优品率；

⑶你认为快乐公司能否通过调整从三个工厂所购买的产品A的比例，使所购买的200件产品A的优品率上升3%．若能，请问应从甲厂购买多少件产品A；若不能，请说明理由．

⑴求快乐公司从丙厂应购买多少件产品Ａ；

28．(10分)快乐公司决定按左图给出的比例，从甲、乙、丙三个工厂共购买200件同种产品A，已知这三个工厂生产的产品A的优品率如右表所示．

甲

乙

丙

优品率

80%

85%

90%

⑵在四边形ABCD中，求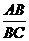的值．

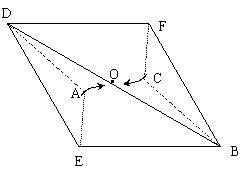⑴求证：四边形ABCD是矩形；

已知：   ABCD的对角线交点为O，点E、F分别在边AB、CD上，分别沿DE、BF折叠四边形ABCD, A、C两点恰好都落在O点处，且四边形DEBF为菱形（如图）．

27．(8分)

26.（7分）1900年，奥地利科学家兰德斯坦纳将人的血液分为A型、B型、AB型和O型四种类型，这就是ABO血型。此后，输血，就成为临床上实际可行的重要治疗措施。输血时，应以输入同型血为原则，也就是每种血型的人可以给自己同血型人输血。但在没有同型血而又情况紧急时，A型和B型的人可以给AB型的人输血，O型的人可以给各种血型的人输血。

（1）根据题意，利用ABO血型之间在输血时的相互关系填写下表（要求：用“+”或“－”填入相应的空格内）：

献血者红细胞（含凝集原）

受血者  血清（含凝集原）

A型（抗B）

B型（抗A）

AB型（无）

O型（抗A、抗B）

A型（A）

－

＋

－

＋

B型（B）

＋

－

＋

A、B型（A、B）

＋

－

＋

O型（无）

－

－

－

－

注：“+”表示有凝集反应，“－”表示无凝集反应。

（2）一个O型血的人需要紧急输血，现有18人请求献血。其中，与A型血发生凝集者为9人，与B型血发生凝集者为7人，与A、B型血都发生凝集者和不发生凝集者共有8人。求这18人中可以实施献血的是几个人？