（2）当点在线段上，且时，其它条件不变．

（1）如图（），当点在线段上时，试判断与的大小关系，并证明你的结论；

27．已知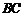为⊙O直径，是直径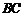上一动点（不与点重合），过点作直线交⊙O于两点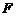，是⊙O上一点（不与点重合），且=，直线交直线于点．

（2）如果每天精加工的蔬菜和没来得及精加工的蔬菜全部售出的利润为元，求与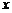的函数关系式，并说明如何安排精加工人数才能使一天所获的利润最大？最大利润是多少？

七、（14分）

（1）求每天蔬菜精加工后再出售所得利润（元）与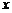（人）的函数关系式；

26．某蔬菜基地加工厂有工人100人，现对100人进行工作分工，或采摘蔬菜，或对当日采摘的蔬菜进行精加工．每人每天只能做一项工作．若采摘蔬菜，每人每天平均采摘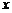48kg；若对采摘后的蔬菜进行精加工，每人每天可精加工32kg（每天精加工的蔬菜和没来得及精加工的蔬菜全部售出）．已知每千克蔬菜直接出售可获利润1元，精加工后再出售，每千克可获利润3元．设每天安排名工人进行蔬菜精加工．

（3）求四边形的面积．

六、（12分）

（2）用配方法求抛物线的顶点的坐标和对称轴；

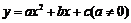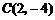25．如图，已知抛物线经过，三点，且与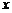轴的另一个交点为．

（1）求抛物线的解析式；

24．如图，某人在山坡坡脚处测得电视塔尖点的仰角为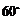，沿山坡向上走到处再测得点的仰角为，已知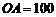米，山坡坡度且在同一条直线上．求电视塔的高度以及此人所在位置点的铅直高度．（测倾器高度忽略不计，结果保留根号形式）

五、（12分）