
1.(-4)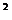 的平方根是
的平方根是
A.4 B.±4 C.-4 D.±8
(3)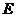 是第二象限内到
是第二象限内到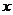 轴、
轴、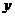 轴的距离的比为5:2的点,如果点E在(2)中的抛物线上,且它与点A在此抛物线对称轴的同侧.问:在抛物线的对称轴上,是否存在点P,使
轴的距离的比为5:2的点,如果点E在(2)中的抛物线上,且它与点A在此抛物线对称轴的同侧.问:在抛物线的对称轴上,是否存在点P,使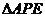 朋的周长最小?若存在,求山点P的坐标;若不存在,请说明理由.
朋的周长最小?若存在,求山点P的坐标;若不存在,请说明理由.
(2)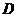 是抛物线与
是抛物线与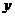 轴的交点,
轴的交点,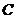 是抛物线上的一点,且以
是抛物线上的一点,且以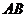 为一底的梯形
为一底的梯形 的面积为9,求此抛物线的解析式;
的面积为9,求此抛物线的解析式;
(1)求抛物线与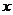 轴的另一个交点
轴的另一个交点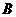 的坐标;
的坐标;
25.已知:抛物线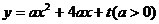 与
与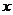 轴的一个交点为
轴的一个交点为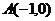 .
.
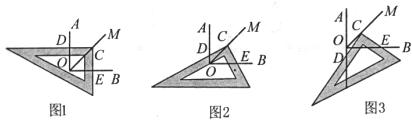
(本小题满分12分)
(2)当三角板绕点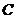 继续旋转到图3这种情况下,上述结论是否还成立?若成立,请给予 证明;若不成立,线段
继续旋转到图3这种情况下,上述结论是否还成立?若成立,请给予 证明;若不成立,线段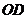 、
、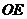 、
、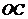 之间又有怎样的数量关系?请写出你的猜想(不必证明)
之间又有怎样的数量关系?请写出你的猜想(不必证明)
(1)当三角板绕点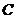 旋转到
旋转到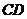 与
与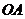 不垂直时,如在图2这种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段
不垂直时,如在图2这种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段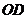 、
、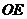 、
、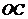 之间又有怎样的数量关系?请写出你的猜想,并证明.
之间又有怎样的数量关系?请写出你的猜想,并证明.
当三角板绕点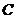 旋转到
旋转到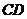 与
与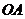 垂直时(如图1),易证结论:
垂直时(如图1),易证结论: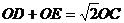 .
.
重合,它的两条直角边分别与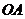 、
、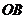 (或它们的反向延长线)相交于点
(或它们的反向延长线)相交于点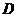 、
、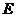 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com