（A）      （B）      

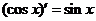
2、下列各式正确的是   （   ） 

  A.  0.3        B . 0.6           C. 0.9           D. 1.2 

1、 已知f(x)=3x²+5,则从0.1到0.2的平均变化率为（  ）

18．解：（Ⅰ）从8人中选出日语、俄语和韩语志愿者各1名，其一切可能的结果组成的基本事件空间

{，，

，，，

，，，

}

由18个基本事件组成．由于每一个基本事件被抽取的机会均等，因此这些基本事件的发生是等可能的．

用表示“恰被选中”这一事件，则

{，

}

事件由6个基本事件组成，

因而．

（Ⅱ）用表示“不全被选中”这一事件，则其对立事件表示“全被选中”这一事件，

由于{}，事件有3个基本事件组成，

所以，由对立事件的概率公式得．

19．（Ⅰ）证明：在中，

由于，，，

所以．

故．

又平面平面，平面平面，

平面，

所以平面，

又平面，

故平面平面．

（Ⅱ）解：过作交于，

由于平面平面，

所以平面．

因此为四棱锥的高，

又是边长为4的等边三角形．

因此．

在底面四边形中，，，

所以四边形是梯形，在中，斜边边上的高为，

此即为梯形的高，

所以四边形的面积为．

故．

20．（Ⅰ）证明：由已知，当时，，

又，

所以，

即，

所以，

又．

所以数列是首项为1，公差为的等差数列．

由上可知，

即．

所以当时，．

因此

（Ⅱ）解：设上表中从第三行起，每行的公比都为，且．

因为，

所以表中第1行至第12行共含有数列的前78项，

故在表中第13行第三列，

因此．

又，

所以．

记表中第行所有项的和为，

则．

21．解：（Ⅰ）因为

，

又和为的极值点，所以，

因此

解方程组得，．

（Ⅱ）因为，，

所以，

令，解得，，．

因为当时，；

当时，．

所以在和上是单调递增的；

在和上是单调递减的．

（Ⅲ）由（Ⅰ）可知，

故，

令，

则．

令，得，

因为时，，

所以在上单调递减．

故时，；

因为时，，

所以在上单调递增．

故时，．

所以对任意，恒有，又，

因此，

故对任意，恒有．

22．解：（Ⅰ）由题意得

又，

解得，．

因此所求椭圆的标准方程为．

（Ⅱ）（1）假设所在的直线斜率存在且不为零，设所在直线方程为，

．

解方程组得，，

所以．

设，由题意知，

所以，即，

因为是的垂直平分线，

所以直线的方程为，

即，

因此，

又，

所以，

故．

又当或不存在时，上式仍然成立．

综上所述，的轨迹方程为．

（2）当存在且时，由（1）得，，

由解得，，

所以，，．

解法一：由于

，

当且仅当时等号成立，即时等号成立，此时面积的最小值是．

当，．

当不存在时，．

综上所述，的面积的最小值为．

解法二：因为，

又，，

当且仅当时等号成立，即时等号成立，

此时面积的最小值是．

当，．

当不存在时，．

综上所述，的面积的最小值为．

分别为验证知在点时取得最大值11.

17．解：（Ⅰ）

．

因为为偶函数，

所以对，恒成立，

因此．

即，

整理得．

因为，且，

所以．

又因为，

故．

所以．

由题意得，所以．

故．

因此．

（Ⅱ）将的图象向右平移个单位后，得到的图象，

所以．

当（），

即（）时，单调递减，

因此的单调递减区间为（）．

16．设满足约束条件 则的最大值为         ．

解析：本小题主要考查线性规划问题。作图(略)易知可行域为一个四角形,其四个顶点

15．已知，

则

的值等于         ．

解析：本小题主要考查对数函数问题。

13．已知圆．以圆与坐标轴的交点分别作为双曲线的一个

焦点和顶点，则适合上述条件的双曲线的标准方程为           ．

解析：本小题主要考查圆、双曲线的性质。圆

得圆与坐标轴的交点分别为

则所以双曲线的标准方程为

则输出的         ．

解析：本小题主要考查程序框图。

，因此输出

11．若圆的半径为1，圆心在第一象限，且与直线和轴相切，

则该圆的标准方程是（  B  ）

A．              B．

C．                 D．

解析：本小题主要考查圆与直线相切问题。

设圆心为由已知得选B.

则满足的关系是（  A  ）

A．             B．

C．             D．

解析：本小题主要考查正确利用对数函数的图象来比较大小。

由图易得取特殊点

      .选A.