
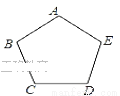
��ͼ���������ABCDE����ijƽ��ֱ������ϵ��������A��B��C��
D������ֱ��ǣ�0��a��������3��2������b��m������c��m�������E������
��__________ .
 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶����ĩͳһ���������ѧ�Ծ� ���ͣ������
ijʵ��ѧУΪ�˽����꼶1200��ѧ�����ʽ�����������г�ȡ��100��ѧ�����в��ԣ� ����������У�����������________��
100 ����������������������������������100��ѧ���Ľ������������������100. �ʴ�Ϊ�� 100.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���½���³ľ����2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ͼ����֪�߶�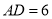 cm���߶�
cm���߶�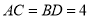 cm��
cm�� 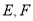 �ֱ����߶�
�ֱ����߶� ���е㣬��
���е㣬��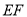 �ij��ȣ�
�ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���½���³ľ����2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ͼ�����߳�Ϊ3a�������������������������κ����鳤���Σ����õ��߳�2b��С�����κ��ٽ�ʣ�µ�����ƴ��һ����Σ��������νϳ��ı߳�Ϊ��������
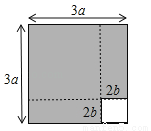
A. 3a+2b B. 3a+4b C. 6a+2b D. 6a+4b
A ���������������� �������У�3a��2b+2b��2=3a��2b+4b=3a+2b�� �������νϳ��ı߳�Ϊ3a+2b����ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ��������2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ͼ����֪��AD�ǡ�ABC�Ľ�ƽ���ߣ�CE�ǡ�ABC�ĸߣ���BAC=60�㣬��BCE=40�㣬���ADB�Ķ�����
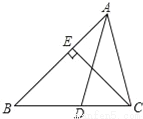
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ��������2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
����ʽ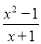 ��ֵΪ0����
��ֵΪ0����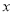 ��ֵ��������������
��ֵ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ��������2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
����a•a5����2a3��2�Ľ��Ϊ��������
A. a6��2a5 B. ��a6 C. a6��4a5 D. ��3a6
D �����������������ͬ��������ˣ��������䣬ָ����ӣ��ݵij˷����������䣬ָ�����.ԭʽ=.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������У2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ͼ��һ��Բ��һֻ���������ڱ���������ֵĵ�����Ծ������ͣ���������ϣ�����һ����˳ʱ�뷽���������㣻��ͣ��ż�����ϣ�����һ������ʱ�뷽����һ���㣬�������2��㿪ʼ������2017��������ͣ����____��Ӧ�ĵ��ϣ�
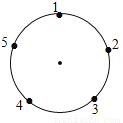
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ̩����2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ѧϰ�˶��θ�ʽ��С��ͬѧ�����еĶ��θ�ʽ����д����һ�����θ�ʽ��ƽ������ʽ.
���磺 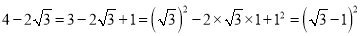 .���ڶ��Ե�С������̽����
.���ڶ��Ե�С������̽����
��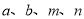 Ϊ������ʱ����
Ϊ������ʱ���� ������
������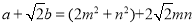 ������
������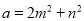 ��
�� 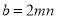 .
.
��ģ��С���ķ���̽��������������⣺
��1����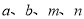 Ϊ������ʱ����
Ϊ������ʱ����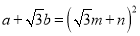 �����ú���
�����ú���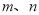 ��ʽ�ӷֱ��ʾ
��ʽ�ӷֱ��ʾ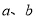 ���ã�
���ã�  ��
�� 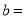 ��
��
��2����գ� 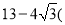

- 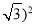 ��
��
��3����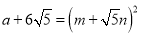 ����
����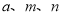 ����������
Ϊ����������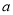 ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com