
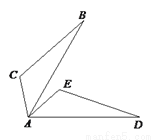
如图,△ABC≌△ADE,AB=AD,AC=AE,∠B=20°,∠E=110°,∠EAB=15°,则∠BAD的度数为______________.
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源:黄金30题系列 八年级数学 小题好拿分 题型:填空题
已知四个数:3-2,-32,30,(-3)3其中最大的数是___.
30 【解析】试题解析:3-2=,-32=-,30=1,(-3)3=-27 ∵1>>->-27 ∴最大的数是30查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级北师大版数学试卷(C卷) 题型:单选题
如图所示图形中,不是正方体的展开图的是( )
A. 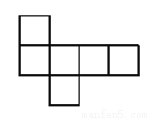 B.
B. 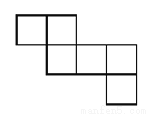
C. 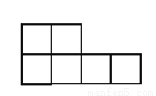 D.
D. 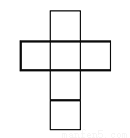
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级北师大版数学试卷(A卷) 题型:单选题
如图,直线AB,CD相交于点O,射线OM平分∠AOC,∠MON=90°,若∠AOM=35°,则∠CON的度数为( )
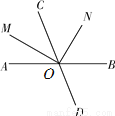
A. 35° B. 45° C. 55° D. 65°
C 【解析】∵射线OM平分∠AOC,∠AOM=35°, ∴∠MOC=35°. ∵∠MON=90°. ∴∠CON=∠MON-∠MOC=90°-35°=55°. 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级北师大版数学试卷(A卷) 题型:单选题
如图是一个正方体的表面展开图,若正方体中相对的面上的数或式子互为相反数,则2x+y的值为( )

A. 0 B. -1 C. -2 D. 1
B 【解析】【解析】 正方体的表面展开图,相对的面之间一定相隔一个正方形.“5”与“2x﹣3”是相对面,“y”与“x”是相对面,“﹣2”与“2”是相对面,∵相对的面上的数字或代数式互为相反数,∴2x﹣3+5=0,x+y=0,解得x=﹣1,y=1,∴2x+y=2×(﹣1)+1=﹣2+1=﹣1.故选B.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 小题好拿分 题型:单选题
如图,a,b,c分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是( )
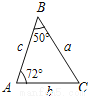
A. 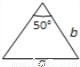 B.
B. 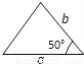 C.
C. 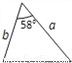 D.
D. 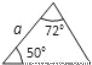
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
观察下列方程的特征及其解的特点.
①x+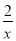 =-3的解为x1=-1,x2=-2;
=-3的解为x1=-1,x2=-2;
②x+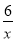 =-5的解为x1=-2,x2=-3;
=-5的解为x1=-2,x2=-3;
③x+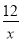 =-7的解为x1=-3,x2=-4.
=-7的解为x1=-3,x2=-4.
解答下列问题:
(1)请你写出一个符合上述特征的方程为____________,其解为x1=-4,x2=-5;
(2)根据这类方程特征,写出第n个方程为________________,其解为x1=-n,x2=-n-1;
(3)请利用(2)的结论,求关于x的方程x+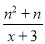 =-2(n+2)(其中n为正整数)的解.
=-2(n+2)(其中n为正整数)的解.
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
已知,抛物线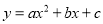 ( a≠0)经过原点,顶点为A(h,k)(h≠0).
( a≠0)经过原点,顶点为A(h,k)(h≠0).
(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线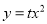 (t≠0)也经过A点,求a与t之间的关系式;
(t≠0)也经过A点,求a与t之间的关系式;
(3)当点A在抛物线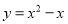 上,且-2≤h<1时,求a的取值范围.
上,且-2≤h<1时,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com