
科目:初中数学 来源:南京市玄武区2016~2017学年度第一学期期九年级试卷 题型:解答题
已知二次函数y=x2+(k-1)x-2k-3.
(1)求证:该二次函数图像与x轴总有两个公共点;
(2)若点A(-1,y1)、B(1,y2)在该二次函数的图像上,且y1>y2,求k的取值范围.
(1)答案见解析;(2)k<1. 【解析】分析:(1)根据△恒大于0即可证明;(2)将x=-1和x=1代入y=x2+(k-1)x-2k-3,再根据,可得结果. 本题解析: (1)由题意得,令,得到方程 a=1,b=k﹣1,c=﹣2k﹣3,则b2﹣4ac=(k﹣1)2﹣4(﹣2k﹣3)=k2+6k+13=(k+3)2+4,. ∵,∴(k+3)2+4>0,即,∴方程有两个...查看答案和解析>>
科目:初中数学 来源:南京市溧水区2016~2017学年度第一学期期末九年级试卷 题型:填空题
将二次函数y= x2的图像向右平移1个单位长度,再向下平移2个单位长度,得到的函数图像的对称轴是_______________
过点(1,2)且平行于y轴的直线;(或直线x=1) 【解析】∵抛物线y=x²向右平移1个单位长度,再向下平移2个单位长度, ∴平移后的解析式为:y=(x?1)²?2. ∴函数图像的对称轴是过点(1,2)且平行于y轴的直线;(或直线x=1), 故答案为:过点(1,2)且平行于y轴的直线;(或直线x=1)查看答案和解析>>
科目:初中数学 来源:广东省揭阳市揭西县2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
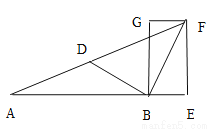
如图,△AEF是直角三角形,∠AEF=900,B为AE上一点,BG⊥AE于点B,GF∥BE,且AD=BD=BF,∠BFG=600,则∠AFG的度数是___________。
查看答案和解析>>
科目:初中数学 来源:广东省揭阳市揭西县2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
下列各组数中,是方程2x-y=8的解的是( )
A. 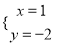 B.
B. 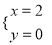 C.
C. 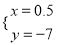 D.
D. 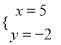
查看答案和解析>>
科目:初中数学 来源:北京市东城区2017-2018学年度第一学期期末教学目标检测初二数学试卷 题型:解答题
北京第一条地铁线路于1971年1月15日正式开通运营.截至2017年1月,北京地铁共有19条运营线路,覆盖北京市11个辖区.据统计,2017 年地铁每小时客运量是2002年地铁每小时客运量的4倍,2017年客运240万人所用的时间比2002年客运240万人所用的时间少30小时,求2017年地铁每小时的客运量?
24万人 【解析】试题分析:设2002年地铁每小时客运量x万人,则2017年地铁每小时客运量4x万人,根据等量关系“2002年客运240万人所用的时间-30=2017年客运240万人所用的时间”列出方程,解方程即可. 试题解析: 设2002年地铁每小时客运量x万人,则2017年地铁每小时客运量4x万人, 由题意得, , 解得x=6. 经检验x=6是分式方程...查看答案和解析>>
科目:初中数学 来源:北京市东城区2017-2018学年度第一学期期末教学目标检测初二数学试卷 题型:填空题
阅读下面材料:
在数学课上,老师提出如下问题:
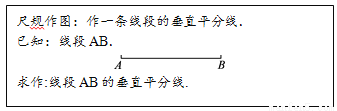
小红的作法如下:

老师说:“小红的作法正确.”
请回答:小红的作图依据是_________________________.
到线段两个端点距离相等的点在这条线段的垂直平分线上,两点确定一条直线. 【解析】根据小红的作图方法可得小红的作图依据是到线段两个端点距离相等的点在这条线段的垂直平分线上,两点确定一条直线.查看答案和解析>>
科目:初中数学 来源:北京市东城区2017-2018学年度第一学期期末教学目标检测初二数学试卷 题型:单选题
世界上最小的鸟是生活在古巴的吸蜜蜂鸟,它的质量约为0.056盎司。将0.056用科学记数法表示为( )
A. 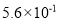 B.
B. 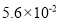 C.
C. 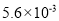 D.
D. 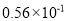
查看答案和解析>>
科目:初中数学 来源:北京市西城区2017-2018学年度第一学期期末考试七年级数学试卷 题型:解答题
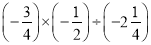
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com