
写出下列图中x的值:
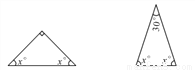
(1)x=______.(2)x=______.
45 75 【解析】(1)∵2x°+90°=180°,∴x=45. (2)∵2x°+30°=180°,∴x=75. 故答案为:(1)45;(2)75. 口算能手系列答案
口算能手系列答案科目:初中数学 来源:人教版九年级上册数学 22.2二次函数与一元二次方程 练习 题型:单选题
二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )
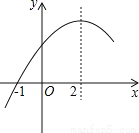
A.1个 B.2个 C.3个 D.4个
B 【解析】 试题分析:根据抛物线的对称轴为直线x=﹣=2,则有4a+b=0;观察函数图象得到当x=﹣3时,函数值小于0,则9a﹣3b+c<0,即9a+c<3b;由于x=﹣1时,y=0,则a﹣b+c=0,易得c=﹣5a,所以8a+7b+2c=8a﹣28a﹣10a=﹣30a,再根据抛物线开口向下得a<0,于是有8a+7b+2c>0;由于对称轴为直线x=2,根据二次函数的性质得到当x>2时...查看答案和解析>>
科目:初中数学 来源:初一数学第一学期4.1线段、直线、射线 同步练习 题型:填空题
如图,图中有__条直线,有__条射线,有__条线段,以E为顶点的角有__个.
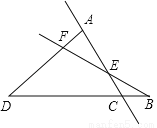
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.2.2中心对称图形 测试 题型:单选题
下列标志图中,既是轴对称图形,又是中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期人教版八年级数学上11.2.1《三角形的内角和》同步练习题(含答案) 题型:填空题
在△ABC中,∠A=∠B+∠C,则∠A=______.
90° 【解析】∵∠A=∠B+∠C,∠A+∠B+∠C=180°, ∴2∠A=180°, ∴∠A=90°, 故答案为:90°.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期人教版八年级数学上11.2.1《三角形的内角和》同步练习题(含答案) 题型:单选题
在△ABC中,∠B=40°,∠C=80°,则∠A的度数为( )
A. 30° B. 40° C. 50° D. 60°
D 【解析】由三角形内角和定理得∠A=180°?∠B?∠C=180°?40°?80°=60°, 故选:D.查看答案和解析>>
科目:初中数学 来源:2018年春九年级数学下册湘教版:单元测试(四) 概率 题型:解答题
下列事件,哪些是必然事件,哪些是不可能事件,哪些是随机事件?
(1)用长度分别为2 dm,3 dm,5 dm的三根钢筋,首尾相连能焊成一个三角形;
(2)如果两个角相等,那么这两个角是对顶角;
(3)任意画一个三角形,其内角和是180°.
(1)是不可能事件.(2)是随机事件.(3)是必然事件. 【解析】试题分析:(1)根据三角形的三边关系可判断; (2)根据对顶角的概念可判断; (3)根据三角形的内角和定理可判断. 试题解析:(1) 根据三角形的三边关系,两边之和大于第三边,可由2+3=5知是不可能事件. (2)根据对顶角的概念,有公共地点,一个角的两边是另一角的两边的反向延长线,故可知两角相等有可能...查看答案和解析>>
科目:初中数学 来源:山西省大同市矿区2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
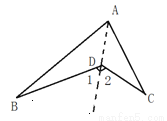
(本题共10分)AB和AC 相交于点A, BD和CD相交于点D,探究∠BDC与∠B 、 ∠C、∠BAC的关系.
小明是这样做的:
解:以点A为端点作射线AD.
∵∠1是△ABD的外角,∴∠1= ∠B+∠BAD.
同理∠2=∠C+∠CAD.
∴∠1+∠2=∠B+∠BAD+∠C+∠CAD.即∠BDC=∠B+∠C+∠BAC.
小英的思路是:延长BD交AC于点E.
(1)按小英的思路完成∠BDC=∠B+∠C+∠BAC这一结论.

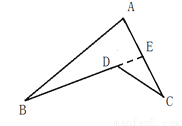
(2)按照上面的思路解决如下问题:如图:在△ABC中,BE、CD分别是∠ABC∠ACB的角平分线,交AC于E,交AB于D.BE、CD相交于点O,∠A=60°.求∠BOC的度数.
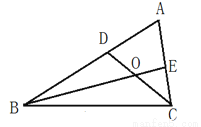
(3)如图:△ABC中,BO、CO分别是∠ABC与∠ACB的角平分线,且BO、CO相交于点O.猜想∠BOC与∠A有怎样的关系,并加以证明.
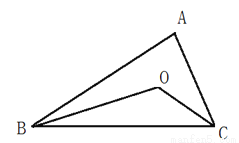
查看答案和解析>>
科目:初中数学 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.1 二次函数 题型:单选题
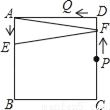
如图,正方形ABCD的边长为4,点P、Q分别是CD、AD的中点,动点E从点A向点B运动,到点B时停止运动;同时,动点F从点P出发,沿P→D→Q运动,点E、F的运动速度相同.设点E的运动路程为x,△AEF的面积为y,能大致刻画y与x的函数关系的图象是( )
A. 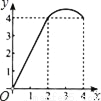 B.
B. 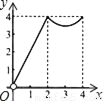 C.
C. 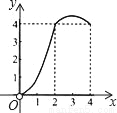 D.
D. 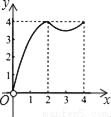
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com