
解方程组:
(1)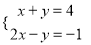 ;(2)
;(2) .
.
科目:初中数学 来源:安徽省淮南市潘集区2017-2018学年八年级上学期第二次联考数学试卷 题型:填空题
若x2+(m﹣3)x+16是完全平方式,则m=__________.
11或-5 【解析】∵x2+(m﹣3)x+16是完全平方式, ∴m-3=±8, ∴m=11或-5.查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(六) 题型:解答题
如图,在平面直角坐标系中,直线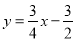 与抛物线
与抛物线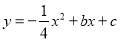 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.
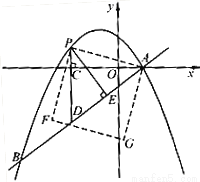
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作如图所示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,求出对应的点P的坐标.
(1)(2)①15 ② 【解析】试题分析:(1)利用直线解析式求出点A、B的坐标,再利用待定系数法求二次函数解析式解答;(2)①利用直线解析式和抛物线解析式表示出PD,再利用同角的余角相等求出∠DPE=∠BAO,根据直线k值求出∠BAO的正弦和余弦值,然后表示出PE、DE,再根据三角形的周长公式列式整理即可得解,再根据二次函数的最值问题解答;②分(i)点G在y轴上时,过点P作PH⊥x轴于H,...查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(六) 题型:单选题
矩形ABCD中,AB=8,BC=3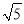 ,点P在边AB上,且BP=3AP,如果圆P是以点P为圆心,PD为半径的圆,那么下列判断正确的是( )
,点P在边AB上,且BP=3AP,如果圆P是以点P为圆心,PD为半径的圆,那么下列判断正确的是( )
A. 点B、C均在圆P外 B. 点B在圆P外、点C在圆P内
C. 点B在圆P内、点C在圆P外 D. 点B、C均在圆P内
C 【解析】试题分析:矩形ABCD中,AB=8, ,点P在边AB上,且BP=3AP,∴AP=2,BP="6,AD=BC." 如果圆P是以点P为圆心,PD为半径的圆;在中有勾股定理得 ,∵PD=7>BP=6,PD=7查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(六) 题型:单选题
2017的倒数是( )
A. 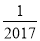 B. 2017 C. ﹣2017 D. ﹣
B. 2017 C. ﹣2017 D. ﹣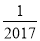
查看答案和解析>>
科目:初中数学 来源:甘肃省张掖市高台县2016-2017学年八年级(上)期末数学试卷 题型:填空题
在y轴上,位于原点的下方,且距离原点4个单位长度的点的坐标是______.
(0,﹣4). 【解析】试题解析:∵点在y轴上, ∴点的横坐标为0, 而点位于原点的下侧,距离原点4个单位长度, ∴点的纵坐标为?4, ∴点的坐标为(0,?4). 故答案为:(0,?4).查看答案和解析>>
科目:初中数学 来源:甘肃省张掖市高台县2016-2017学年八年级(上)期末数学试卷 题型:单选题
如图,一个圆桶儿,底面直径为16cm,高为18cm,则一只小虫底部点A爬到上底B处,则小虫所爬的最短路径长是(π取3)( )
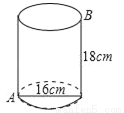
A. 20cm B. 30cm C. 40cm D. 50cm
B 【解析】试题分析:先将圆柱的侧面展开为一矩形,而矩形的长就是底面周长的一半,高就是圆柱的高,再根据勾股定理就可以求出其值. 【解析】 展开圆柱的侧面如图,根据两点之间线段最短就可以得知AB最短. 由题意,得AC=3×16÷2=24, 在Rt△ABC中,由勾股定理,得 AB===30cm. 故选B.查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级上期末复习检测数学试卷 题型:填空题
如果a,b互为相反数,c,d互为倒数,x的绝对值等于2,那么x2+cdx﹣a﹣b的值是________.
6或2 【解析】∵a,b互为相反数,c,d互为倒数,x的绝对值等于2, ∴a+b=0,cd=1,x=±2, 当x=2时,原式=4+2﹣0=6; 当x=﹣2时,原式=4﹣2﹣0=2, 故答案为:6或2.查看答案和解析>>
科目:初中数学 来源:重庆市江北区2018届九年级上期末模拟数学试卷 题型:单选题
如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( )
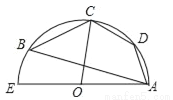
A. 40° B. 60° C. 70° D. 80°
D 【解析】试题分析:根据圆内接四边形的性质求出∠B的度数,根据圆周角定理得到答案. 【解析】 ∵四边形ABCD是圆内接四边形, ∴∠ADC+∠B=180°,又∠ADC=140°, ∴∠B=40°, ∴∠AOC=2∠B=80°, 故选:D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com