练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

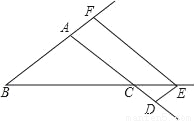
    在△ABC中，AB=AC，点D、E、F分别是AC、BC、BA延长线上的点，四边形ADEF为平行四边形．求证：AD=BF．

    证明见解析. 【解析】证明：∵四边形ADEF为平行四边形， ∴AD=EF，AD∥EF， ∴∠ACB=∠FEB， ∵AB=AC， ∴∠ACB=∠B， ∴∠FEB=∠B， ∴EF=BF， ∴AD=BF．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年山东省中考数学二模试卷 题型：单选题

    数学活动课上，小敏、小颖分别画了△ABC和△DEF，数据如图，如果把小敏画的三角形面积记作S△ABC，小颖画的三角形面积记作S△DEF，那么你认为（　　）

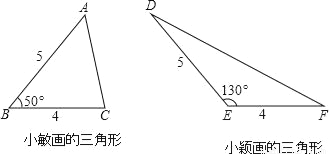
    A. S△ABC＞S△DEF B. S△ABC＜S△DEF C. S△ABC=S△DEF D. 不能确定

    C 【解析】试题解析：如图，过点A.D分别作AG⊥BC，DH⊥EF，垂足分别为G、H， 在Rt△ABG中, 在Rt△DHE中, ∴AG=DH. ∵BC=4，EF=4， 故选C.

    查看答案和解析>>

    科目：初中数学 来源：福建省建瓯市2018届九年级数学上册期末测试卷 题型：解答题

    如图，在Rt△ABC中，∠ABC＝90°，以AB为直径作半圆⊙O交AC于点D，点E为BC的中点，连接DE.

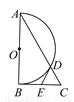
    (1)求证：DE是半圆⊙O的切线；

    (2)若∠BAC＝30°，DE＝2，求AD的长．

    (1)证明见解析;(2) AD＝6. 【解析】试题分析：（1）连接OD，OE，由AB为圆的直径得到三角形BCD为直角三角形，再由E为斜边BC的中点，得到DE=BE=DC，再由OB=OD，OE为公共边，利用SSS得到三角形OBE与三角形ODE全等，由全等三角形的对应角相等得到DE与OD垂直，即可得证； （2）在直角三角形ABC中，由∠BAC=30°，得到BC为AC的一半，根据BC=2DE...

    查看答案和解析>>

    科目：初中数学 来源：福建省建瓯市2018届九年级数学上册期末测试卷 题型：单选题

    从图中的四张印有汽车品牌标志图案的卡片中任取一张，取出印有汽车品牌标志的图案是中心对称图形的卡片的概率是（　　）

    A. B. C. D. 1

    A 【解析】试题分析：在这四个图片中只有第三幅图片是中心对称图形，因此是中心对称称图形的卡片的概率是． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：解答题

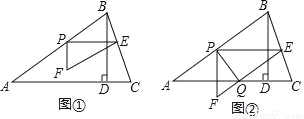
    如图①，在锐角△ABC中，AB=5，tanC=3，BD⊥AC于点D，BD=3，点P从点A出发，以每秒1个单位长度的速度沿AB向终点B运动，过点P作PE∥AC交边BC于点E，以PE为边作Rt△PEF，使∠EPF=90°，点F在点P的下方，且EF∥AB．设△PEF与△ABD重叠部分图形的面积为S（平方单位）（S＞0），点P的运动时间为t（秒）（t＞0）．

    （1）求线段AC的长．

    （2）当△PEF与△ABD重叠部分图形为四边形时，求S与t之间的函数关系式．

    （3）若边EF与边AC交于点Q，连结PQ，如图②．

    ①当PQ将△PEF的面积分成1：2两部分时，求AP的长．

    ②直接写出PQ的垂直平分线经过△ABC的顶点时t的值．

    （1）5；（2）当0＜t≤1时，S=t2+t；当≤t＜5时，S=（5﹣t）2；（3）①或；②或. ． 【解析】试题分析： （1）在Rt△ABD中，由∠BDA=90°，AB=5，BD=3，可由勾股定理求得AD=4；在Rt△BCD中，∠BDC=90°，BD=3，tanc=3，可求得CD=1；由此可得AC=AD+CD=5； （2）由题意分析可知，如图1，当点D在线段EF上或EF的...

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：填空题

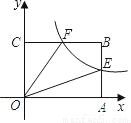
    如图，在平面直角坐标系中，函数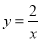（x＞0）的图象经过矩形OABC的边AB、BC的中点E、F，则四边形OEBF的面积为_____．

    2 【解析】设矩形OABC中点B的坐标为， ∵点E、F是AB、BC的中点， ∴点E、F的坐标分别为： 、， ∵点E、F都在反比例函数的图象上， ∴S△OCF= =，S△OAE=， ∴S矩形OABC= ， ∴S四边形OEBF= S矩形OABC- S△OAE-S△OCF=. 即四边形OEBF的面积为2.

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：单选题

    如图，在△ABC中，AB=AC，过点A作AD∥BC，若∠1=50°，则∠CAD的大小为（　　）

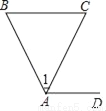
    A. 50° B. 65° C. 80° D. 60°

    B 【解析】∵在△ABC中，AB=AC，∠1=50°， ∴∠C=∠B=， 又∵AD∥BC， ∴∠CAD=∠C=65°. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年度第一学期海南省海口市七年级数学科期末检测模拟 题型：单选题

    如图，点E在AB的延长线上，下列条件中能判断AD∥BC的是（　　）

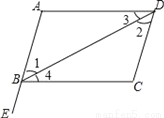
    A. ∠1=∠2 B. ∠3=∠4 C. ∠C=∠CBE D. ∠C+∠ABC=180°

    B 【解析】A. ∵∠1=∠3，∴AB∥CD, 故不正确； B. ∵ ∠2=∠4 , ∴AD∥BC, 故正确； C. ∵∠C=∠CBE , ∴AB∥CD, 故不正确； D. ∵∠C+∠ABC=180º, ∴AB∥CD, 故不正确； 故选B.

    查看答案和解析>>

    科目：初中数学 来源：山东省德州市2018届九年级上期末模拟数学试卷 题型：解答题

    如图，已知抛物线y=﹣x2+2x+3与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，连接BC．

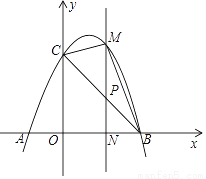
    （1）求A，B，C三点的坐标；

    （2）若点P为线段BC上一点（不与B，C重合），PM∥y轴，且PM交抛物线于点M，交x轴于点N，当△BCM的面积最大时，求点P的坐标；

    （3）在（2）的条件下，当△BCM的面积最大时，在抛物线的对称轴上存在一点Q，使得△CNQ为直角三角形，求点Q的坐标．

    （1）C（0，3），A（﹣1，0），B（3，0）；（2）当t=时，△BCM的面积最大，此时P点坐标为（ ， ）；（3）Q点的坐标为（1， ）或（1， ）或（1， ）或（1，﹣）. 【解析】试题分析：（1）在抛物线解析式中，令x=0可求得C点坐标，令y=0则可求得A、B的坐标；（2）由B、C的坐标可求得直线BC的解析式为y=﹣x+3，可设P点坐标为（t，﹣t+3），则可表示出M点坐标，则可求得...

    查看答案和解析>>

    同步练习册答案