练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若抛物线y＝(x－m)2＋(m＋1)的顶点在第一象限，则m的取值范围为(　　)

    A. m＞1 B. m＞0 C. m＞－1 D. －1＜m＜0

    B 【解析】试题分析：利用y=ax2+bx+c的顶点坐标公式表示出其顶点坐标，根据顶点在第一象限，所以顶点的横坐标和纵坐标都大于0列出不等式组．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖南省醴陵市青云学校2016-2017学年七年级上学期期中考试数学试卷 题型：解答题

    把下列各数填入相应集合内：＋8.5，0.3，0，－3.4，12，－9，4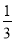，－1.2，－2。

    (1)分数集合： { }；

    (2)正数集合： ｛ ｝；

    (3)非正整数集合：{ }；

    (4)自然数集合： { }．

    见解析 【解析】试题分析：利用分数，正数，整数，非正整数，以及自然数的定义判断即可． 试题解析： (1)分数集合： { +8.5 ，0.3，-3.4，4，-1.2， } (2)正数集合：｛+8.5，0.3，12，4， ｝； (3)非正整数集合：{ 0，-9，-2， } (4)自然数集合： {0，12， }．

    查看答案和解析>>

    科目：初中数学 来源：人教七年级下册数学第九章-不等式与不等式组单元测试 题型：单选题

    不等式x+2<6的非负整数解有（ ）

    A. 2个 B. 3个 C. 4个 D. 5个

    C 【解析】根据不等式的解法，解不等式得x＜4，然后可得非负整数解有0，1，2，3，共4个. 故选：C.

    查看答案和解析>>

    科目：初中数学 来源：2017年秋（北师大版）九年级数学下册（河南）检测：2.2　二次函数的图象与性质 题型：单选题

    二次函数y=ax2+bx+c(a≠0)的大致图象如图，关于该二次函数，下列说法错误的是( )

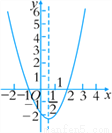
    A. 函数有最小值 B. 对称轴是直线x=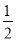

    C. 当x<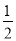时，y随x的增大而减小 D. 当-1<x<2时，y>0

    D 【解析】试题分析：根据抛物线的开口方向，利用二次函数的性质判断A；根据图形直接判断B；根据对称轴结合开口方向得出函数的增减性，进而判断C；根据图象，当-1＜x＜2时，抛物线落在x轴的下方，则y＜0，从而判断D． 试题解析：A、由抛物线的开口向上，可知a＞0，函数有最小值，正确，故A选项不符合题意； B、由图象可知，对称轴为x=，正确，故B选项不符合题意； C、因为a＞0...

    查看答案和解析>>

    科目：初中数学 来源：2017年秋（北师大版）九年级数学下册（河南）检测：2.2　二次函数的图象与性质 题型：解答题

    已知：抛物线．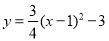

    （1）写出抛物线的开口方向、对称轴；

    （2）函数y有最大值还是最小值？并求出这个最大（小）值；

    （3）设抛物线与y轴的交点为P，与x轴的交点为Q，求直线PQ的函数解析式．

    【解析】 （1）抛物线， ∵a= ＞0， ∴抛物线的开口向上， 对称轴为x=1； （2）∵a=＞0， ∴函数y有最小值，最小值为－3； （3）令x=0，则 ， 所以，点P的坐标为（0， ）， 令y=0，则， 解得x1=-1，x2=3， 所以，点Q的坐标为（-1，0）或（3，0）， 当点P（0， ），Q（-1，0）时，设直线PQ的解析式...

    查看答案和解析>>

    科目：初中数学 来源：2017年秋（北师大版）九年级数学下册（河南）检测：2.2　二次函数的图象与性质 题型：解答题

    先列表，然后在同一平面直角坐标系内分别描点画出下列二次函数的图象，并写出对称轴与顶点坐标．

    ①y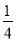＝－ (x＋2)2；②y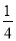＝－ (x－1)2.

    见解析 【解析】试题分析：描点画二次函数图像时，取对称轴两侧的点更容易确定函数图像，根据图像确定：抛物线y＝－ (x＋2)2的对称轴为直线x＝－2，顶点坐标为(－2，0)； 抛物线y＝－ (x－1)2的对称轴为直线x＝1，顶点坐标为(1，0)． 【解析】 列表： x … －4 －3 －2 －1 0 … y＝－ (x＋2)2 ...

    查看答案和解析>>

    科目：初中数学 来源：2017年秋（北师大版）九年级数学下册（河南）检测：2.2　二次函数的图象与性质 题型：解答题

    已知抛物线y＝(m－1)x2＋m2－2m－2的图象开口向下，且经过点(0，1)．

    (1)求m的值；

    (2)求此抛物线的顶点坐标及对称轴；

    (3)当x为何值时，y随x的增大而增大？

    (1) m＝－1；(2) (3) 见解析 【解析】试题分析：开口向下说明m-1<0，将（0,1）代入函数表达式可求出m的值；函数表达式为y＝－2x2＋1，可求得对称轴是y轴，顶点坐标是（0,1）；开口向下，对称轴是y轴，所以在y轴左侧，y随x的增大而增大。 【解析】 (1)由题意，得， 解得m＝－1. (2)当m＝－1时，抛物线的表达式为y＝－2x2＋1，其顶点坐标为(0...

    查看答案和解析>>

    科目：初中数学 来源：2017年秋（北师大版）九年级数学下册（河南）检测：2.2　二次函数的图象与性质 题型：解答题

    如图所示，拱桥是抛物线形，其函数表达式为y＝－x2，当水位线在AB位置时，水面的宽AB是6 m，求这时水面离拱形顶部的高度OC.

    9m. 【解析】试题分析：由函数图象及函数表达式可得函数图像对称轴是y轴，A、B两点关于y轴互相对称，所以可以得到BC=3m，所以B点横坐标为3，将x=3代入函数表达式得到B点纵坐标，y=-9，所以可得到高度OC=9m 【解析】 ∵AB＝6m，∴BC＝3m. ∴B点的横坐标为3，则纵坐标为y＝－32＝－9. ∴OC＝9m. 答：这时水面离拱形顶部的高度OC为9m. ...

    查看答案和解析>>

    科目：初中数学 来源：湖南省耒阳市冠湘学校2018届九年级上学期第二次段考（期中）考试数学试卷 题型：解答题

    △ABC中，∠ACB=90°，CD⊥AB于D，AE平分∠CAB交CD于F，CH⊥EF于H，连接DH，求证：(1)EH=FH；

    (2)∠CAB=2∠CDH．

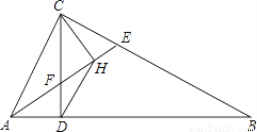
    （1）证明见解析（2）证明见解析 【解析】试题分析：（1）根据余角的性质得到∠AFD＝∠AEC，证得∠CFE＝∠CEF，得到CF＝CE，根据等腰三角形的性质即可得到结论． （2）由于∠ADF＝∠CHF＝90°，∠AFD＝∠CFH，得到△ADF∽△CFH，根据相似三角形的性质得到，由于∠AFC＝∠DFH，得到△AFC∽△DFH，根据相似三角形的性质得到∠CAF＝∠CDH，等量代换即可得到...

    查看答案和解析>>

    同步练习册答案