
��������ÿ��С�����εı߳�����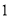 ��
��
�� ����ͼ���еĸ��
����ͼ���еĸ�� �Ƶ�
�Ƶ�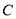 ˳ʱ����ת
˳ʱ����ת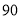 ��������ת�������Σ�
��������ת�������Σ�
��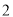 ����ͼ���л�һ�����
����ͼ���л�һ�����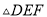 ��ʹ
��ʹ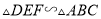 �������Ʊ�Ϊ
�������Ʊ�Ϊ ��
��
�� ����ͼ���л�һ�����
����ͼ���л�һ�����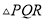 ��ʹ
��ʹ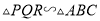 �������Ʊ�Ϊ
�������Ʊ�Ϊ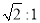 ��
��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�����б�Ӧ��2018����꼶��ѧ��12���¿���ѧ�Ծ� ���ͣ���ѡ��
��ͼ����һ���뾶Ϊ30cm�����Ϊ300��cm2��������Ƥ������һ����Բ��������ģ�����Բ�ĵ���뾶rΪ�� ��
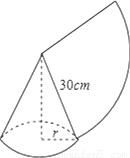
A. 5cm B. 10cm C. 20cm D. 5��cm
B �����������������Բ�ĵ����ܳ�=���εĻ������ݴ��е�ʽ���r��ֵ�� �����r=10cm�� �ʴ�Ϊ��10cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧ��ģ�Ծ� ���ͣ������
��ͼ��A��B�Ƿ��������� ͼ���ϵ����㣬����A��AC��y�ᣬ����ΪC��AC��OB�ڵ�D����DΪOB���е㣬��AOD�����Ϊ3����k��ֵΪ_____��
ͼ���ϵ����㣬����A��AC��y�ᣬ����ΪC��AC��OB�ڵ�D����DΪOB���е㣬��AOD�����Ϊ3����k��ֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ƹ���2017-2018ѧ�����꼶��ѧ�ڵ�����ѧ�������ѧ�Ծ� ���ͣ���ѡ��
��֪|a|=5��b2=16����ab��0����ôa��b��ֵΪ��������
A. ��1 B. ��9 C. 1��9 D. ��1��9
B ���������ߣ� �࣬ �֡ߣ� �൱ʱ�� ����ʱ�� �� ��� ��. ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�������������m��ʵ��ѧУ2018����꼶��ѧ�����п�����ѧ�Ծ����������� ���ͣ������
��ͼ���ڡ�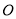 �У���
����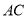 ��
�� 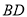 �ཻ�ڵ�
�ཻ�ڵ�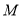 ����
���� ��
��
��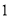 ����֤��
����֤�� 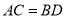 ��
��
��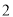 ����
����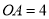 ��
�� 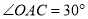 ����
����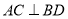 ʱ����
ʱ����
��ͼ����Ӱ���������
�ڻ�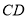 �ij���
�ij���
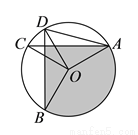
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�������������m��ʵ��ѧУ2018����꼶��ѧ�����п�����ѧ�Ծ����������� ���ͣ������
��֪�����߶εij��ֱ���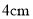 ��
�� 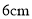 ��
��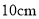 �����ټ�һ��__________
�����ټ�һ��__________ 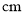 ���߶Σ�����ʹ֮�����߶γɱ�����
���߶Σ�����ʹ֮�����߶γɱ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�������������m��ʵ��ѧУ2018����꼶��ѧ�����п�����ѧ�Ծ����������� ���ͣ���ѡ��
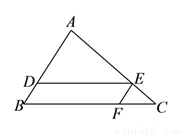
��ͼ����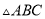 �У���
����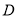 ��
�� 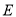 ��
�� 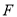 �ֱ��ڱ�
�ֱ��ڱ�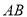 ��
�� 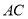 ��
�� 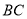 �ϣ���
�ϣ���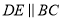 ��
�� 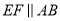 ����
����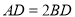 ����
����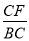 ��ֵΪ�� ����
��ֵΪ�� ����
A. 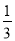 B.
B. 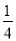 C.
C. 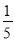 D.
D. 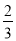
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2017-2018ѧ����꼶12���¿���ѧ�Ծ� ���ͣ���ѡ��
һ�죬����ʦ��ѧУ����ȥ���ᣬ����;����������ֻ�ò��иϵ��᳡����������ֱ�ӻص�ѧУ����ͼ������������ѧУ�ľ���y��ǧ�ף���ʱ��x��ʱ���Ĺ�ϵ��ͼ���ǣ� ��
A. 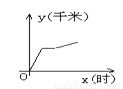 B.
B.  C.
C. 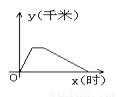 D.
D. 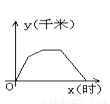
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ������2017-2018ѧ����꼶�ϲ���ĩģ����ѧ�Ծ� ���ͣ������
����ͼ����֪AD��BC����Ҫ��������и�С�⣨������ͼ�ۼ�����Ҫ��д��������
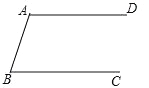
��1����ֱ�ߺ�Բ��������BAD��ƽ����AP����BC�ڵ�P��
��2���ڣ�1���Ļ����ϣ�����APB=55�㣬���B�Ķ�����
��3���ڣ�1���Ļ����ϣ�E��AP���е㣬����BE���ӳ�����AD�ڵ�F������PF����֤���ı���ABPF�����Σ�
�������� �������� �����������1���������� ��ͼ��APΪ������ ��2���������� ��AD��BC�����DAP=��APB=55�㣬��APƽ�֡�DAB�����BAP=��DAP=55�㣬���ABP=180�㩁55�㩁55��=70�㣻 ��2��֤�����ߡ�BAP=��APB����BA=BP����BE=FE��AEƽ�֡�BAF�����ABFΪ���������Σ���AB=AF����AF=BP����AF��BP����...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com