练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    先化简再求值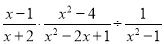： ，请在下列﹣2，﹣1，0，1四个数中任选一个数求值．

    x2﹣x﹣2 ; -2 【解析】试题分析：原式利用除法法则变形，约分得到最简结果，把x=0代入计算即可求出值． 试题解析：原式= =（x﹣2）（x+1）=x2﹣x﹣2， 当x=0时，原式=﹣2．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年湖南省郴州市临武县景山学校中考数学模拟试卷 题型：解答题

    已知y=y1+y2，其中y1与x成正比例，y2与（x﹣2）成反比例．当x=1时，y=2；x=3时，y=10．求：

    （1）y与x的函数关系式；

    （2）当x=﹣1时，y的值．

    （1）y与x的函数关系式为y=3x+；（2）-. 【解析】试题分析： 试题解析： 【解析】 （1）∵y=y1+y2，其中y1与x成正比例，y2与（x﹣2）成反比例， ∴设y1=ax，y2=， ∴y与x的函数关系式为y=ax． 将点（1，2）、（3，10）代入y=ax．中， 得： ，解得： ， ∴y与x的函数关系式为y=3x+. （2）令x=﹣...

    查看答案和解析>>

    科目：初中数学 来源：2017年河北省沧州市中考数学模拟试卷（九） 题型：解答题

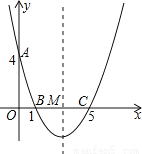
    如图，在直角坐标系中，抛物线经过点A（0，4），B（1，0），C（5，0），其对称轴与x轴相交于点M．

    （1）求抛物线的解析式和对称轴；

    （2）在抛物线的对称轴上是否存在一点P，使△PAB的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由；

    （3）连接AC，在直线AC的下方的抛物线上，是否存在一点N，使△NAC的面积最大？若存在，请求出点N的坐标；若不存在，请说明理由．

    （1）抛物线的解析式为y=x2﹣x+4，对称轴是：直线x=3；（2）P点坐标为（3， ）， 理由见解析；（3）在直线AC的下方的抛物线上存在点N（，﹣3），使△NAC面积最大. 【解析】(1)根据已知条件可设抛物线的解析式为y＝a(x－1)(x－5)． 把点A(0，4)代入上式，解得a＝． ∴y＝ (x－1)(x－5)＝x2－x＋4＝ (x－3)2－． ∴抛物线的对称...

    查看答案和解析>>

    科目：初中数学 来源：2017年河北省沧州市中考数学模拟试卷（九） 题型：单选题

    某小组7位同学的中考体育测试成绩(满分30分)依次为27，30，29，27，30，28，30，则这组数据的众数与中位数分别是( )

    A. 30，27 B. 30，29 C. 29，30 D. 30，28

    B 【解析】试题分析：根据一组数据中出现次数最多的数是众数，所以这组数据的众数是30；按照大小顺序排序后处在中间或者是中间两个数的平均数是中位数，所以这组数据的中位数是29． 故选：B．

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省黄石市中考数学模拟试卷 题型：解答题

    某商店原来将进货价为8元的商品按10元售出，每天可销售200件．现在采用提高售价，减少进货量的方法来增加利润，已知每件商品涨价1元，每天的销售量就减少20件．设这种商品每个涨价x元．

    （1）填空：原来每件商品的利润是__________元，涨价后每件商品的实际利润是__________元（可用含x的代数式表示）；

    （2）为了使每天获得700元的利润，售价应定为多少元？

    （3）售价定为多少元时，每天利润最大，最大利润是多少元？

    （1）2；（2+x）（2）售价应定为13元或15元（3）当涨价4元（即售价为14元）时，每天利润最大，最大利润为720元 【解析】试题分析：（1）根据利润=售价-进价表示出商品的利润即可； （2）设应将售价提为x元时，才能使得所赚的利润最大为y元，根据题意可得：y=（10+x-8）（200-2x），令y=700，解出x的值即可； （3）根据总利润w=单件利润×销售量列出函数表达式...

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省黄石市中考数学模拟试卷 题型：填空题

    若关于x的一元二次方程kx2+4x﹣2=0有两个不相等的实数根，则k的取值范围是_____．

    k＞﹣2且k≠0 【解析】试题解析：根据题意得k≠0且△=42-4•k•（-2）＞0， 所以k＞-2且k≠0． 故答案为k＞-2且k≠0．

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省黄石市中考数学模拟试卷 题型：单选题

    某支青年排球队有12名队员，队员年龄情况如图所示，那么球队队员年龄的众数、中位数分别是（　　）

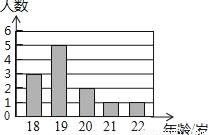
    A. 19，19 B. 19，20 C. 20，20 D. 22，19

    A 【解析】试题解析：由条形统计图可知， 某支青年排球队12名队员年龄的众数是19，中位数是19， 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年内蒙古乌海市七年级（下）期末数学试卷 题型：填空题

    =_____．

    1 【解析】试题解析：原式 故答案为：1.

    查看答案和解析>>

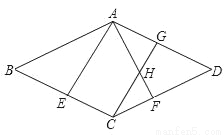
    科目：初中数学 来源：2017年湖北省黄冈市中考数学三模试卷 题型：解答题

    已知：如图，在菱形ABCD中，E、F分别是BC、CD的中点．

    （1）求证：△ABE≌△ADF；

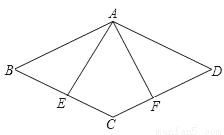
    （2）过点C作CG∥EA交AF于H，交AD于G，若∠BAE=25°，∠BCD=130°，求∠AHC的度数．

    (1)证明见解析；（2）100°. 【解析】试题分析：根据菱形的性质可得AB=AD，∠B=∠D，BE=DF，利用SAS判定△ABE≌△ADF；由△ABE≌△ADF可得∠BAE=∠DAF=25°，从而可推出∠EAF的度数，根据平行线的性质可得到∠AHC的度数． 试题分析：（1）证明：菱形ABCD中，AB=BC=CD=AD，∠B=∠D， ∵E、F分别是BC、CD的中点， ∴BE...

    查看答案和解析>>

    同步练习册答案