
��֪����ͼ��������ABCD�У�E��F�ֱ���BC��CD���е㣮
��1����֤����ABE�ա�ADF��
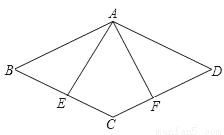
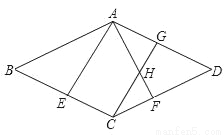
��2������C��CG��EA��AF��H����AD��G������BAE=25�㣬��BCD=130�㣬���AHC�Ķ�����

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�����ʡ��ʯ���п���ѧģ���Ծ� ���ͣ������
�Ȼ�������ֵ�� 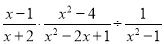 ���������Щ�2����1��0��1�ĸ�������ѡһ������ֵ��
���������Щ�2����1��0��1�ĸ�������ѡһ������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ɹ��ں������꼶���£���ĩ��ѧ�Ծ� ���ͣ���ѡ��
����˵������ȷ���ǣ� ��
A. 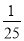 ��ƽ������
��ƽ������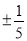 B. ��9��81��һ��ƽ����
B. ��9��81��һ��ƽ����
C. 0.2������ƽ������0.04 D. ��27���������ǣ�3
C �����������������A. ��ƽ������ ����ȷ�� B. ��9��81��һ��ƽ��������ȷ�� C. 0.2����0.04����ƽ���� ������ D. ��27���������ǣ�3����ȷ ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ2017���п���ѧһģ�Ծ� ���ͣ���ѡ��
����ͼ���У��������ĶԳ�ͼ��������Գ�ͼ�ε��ǣ� ��
A���ȱ������� B������ C���������� D��ƽ���ı���
B ��������������Գ�ͼ�εĸ�����һ��ͼ����һ��ֱ���۵���ֱ�����ԵIJ����ܹ������غϣ����ͼ�ν�����Գ�ͼ�Σ�����ֱ�߽����Գ�����ĶԳ�ͼ�εĶ��壺��һ��ͼ����ijһ����ת180�㣬�����ת���ͼ���ܹ���ԭ����ͼ���غϣ���ô���ͼ�ξͽ������ĶԳ�ͼ�Σ����ÿһ��ѡ����з���������ѡ���𰸣� A������Գ�ͼ�Σ��������ĶԳ�ͼ�Σ��ʴ�ѡ����� B������Գ�ͼ�Σ�Ҳ�����ĶԳ�ͼ��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�Ƹ����п���ѧ��ģ�Ծ� ���ͣ������
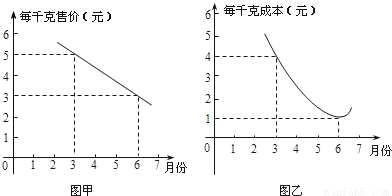
ij�Ϲ������г���Ϊָ���û���ij���߲˵��������ۣ��ڶ������г����������������е���Ļ����ϣ��Խ��������߲����к���г��ۼۺ������ɱ�������Ԥ�⣬�ṩ�������������Ϣ����ͼ��ʾ��ע����ͼ�е�ÿ��ʵ�ĵ�����Ӧ��������ֱ�ָ��Ӧ�·ݵ��ۼۺͳɱ��������ɱ�6�·���ͣ�ͼ��ͼ�����߶Σ�ͼ�ҵ�ͼ���������ߣ�
�������ͼ���ṩ����Ϣ˵����
��1����3�·ݳ��������߲ˣ�ÿǧ�˵������Ƕ���Ԫ��������=�ۼ۩��ɱ���
��2���ĸ��³��������߲ˣ�ÿǧ�˵��������˵�����ɣ�
��3����֪�г������۸����߲ˣ�4��5�����µ�������Ϊ48��Ԫ����5�·ݵ�������4�·ݵ�������2���4��5�����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�Ƹ����п���ѧ��ģ�Ծ� ���ͣ���ѡ��
һ�����ȵ��������������Ϸֱ������1��2��3��4��5��6����ͼ���������������չ��ͼ��������������壬����һ���ϵ���ǡ�õ��ڳ���һ���ϵ����� �ĸ����ǣ�������
�ĸ����ǣ�������

A.  B.
B.  C.
C. 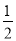 D.
D. 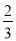
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�Ƹ����п���ѧ��ģ�Ծ� ���ͣ������
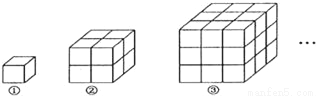
��ͼ���۲����ⳤΪ1��С������ڳɵ�ͼ�Σ�Ѱ�ҹ��ɣ���ͼ���У�����1��С�����壬����1�����ü���0������������ͼ���У�����8��С�����壬����7�����ü���1������������ͼ���У�����27��С�����壬����19�����ü���8����������������ڢ�ͼ�У����ü���С��������_____����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����з���2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ���ѡ��
��ͼ������������y1=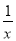 ����κ���y2=ax2+bx+cͼ���ཻ��A��B��C�����㣬����y=ax2+bx-
����κ���y2=ax2+bx+cͼ���ཻ��A��B��C�����㣬����y=ax2+bx- +c��ͼ����X�ύ��ĸ����ǣ� ��
+c��ͼ����X�ύ��ĸ����ǣ� ��
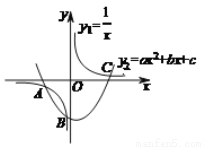
A. 3 B. 2 C. 1 D. 0
A ����������ʱ,��=ax²+bx+c,��ax²+bx?+c=0�� �߷��̵Ľ⼴��������������κ���=ax²+bx+cͼ��ĺ����꣬ �߷���������=����κ���=ax²+bx+cͼ���ཻ��A. B. C�����㣬 �ຯ��y=ax²+bx?+c��ͼ����x�ύ�㼴��ax2+bx?1x+c=0�Ľ⣬ �ຯ��y=ax²+bx?+c��ͼ����x�ύ��ĸ�����3���� ��ѡA....�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ������ʡ���꼶���£��ڶ��β�����ѧ�Ծ� ���ͣ������
��ͼ����C��D���߶�AB�ϵ����㣬��AC=4��CD=5��DB=3����ͼ�������߶εĺ���_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com