
下列各式中, 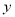 是关于
是关于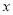 的二次函数的是( ).
的二次函数的是( ).
A. 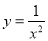 B.
B. 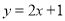 C.
C. 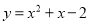 D.
D. 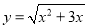
科目:初中数学 来源:山东省2018届九年级上学期第三次月考数学试卷 题型:单选题
在平面直角坐标系中,点(1,﹣2)关于原点对称的点的坐标是( )
A.(1,2) B.(﹣1,2) C.(2,﹣1) D.(2,1)
B 【解析】 试题分析:平面直角坐标系中任意一点P(x,y),关于原点的对称点是(-x,-y),可得点(1,-2)关于原点对称的点的坐标是(-1,2), 故选B.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题好拿分 题型:解答题
在Rt△POQ中,OP=OQ=4,M是PQ中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.
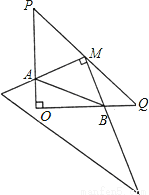
(1)求证:MA=MB;
(2)连结AB,探究:在旋转三角尺的过程中,△AOB的周长是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
(1)证明见解析;(2)有最小值,最小值为4+2. 【解析】 试题分析:(1)过点M作ME⊥OP于点E,作MF⊥OQ于点F,可得四边形OEBF是矩形,根据三角形的中位线定理可得ME=MF,再根据同角的余角相等可得∠AME=∠BMF,再利用“角边角”证明△AME和△BMF全等,根据全等三角形对应边相等即可证明; (2)根据全等三角形对应边相等可得AE=BF,设OA=x,表示出AE为...查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区第十三中学2017-2018学年九年级上学期期中考试数学试卷 题型:填空题
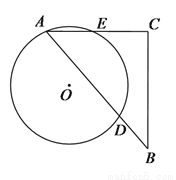
如图,一块含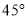 角的直角三角板,它的一个锐角顶点
角的直角三角板,它的一个锐角顶点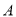 在半径为
在半径为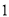 的⊙
的⊙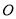 上,边
上,边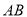 ,
, 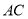 分别与⊙
分别与⊙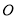 交于点
交于点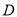 ,
, 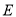 ,则
,则 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区第十三中学2017-2018学年九年级上学期期中考试数学试卷 题型:单选题
抛物线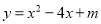 的顶点在
的顶点在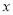 轴上,则
轴上,则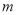 的值为( ).
的值为( ).
A. 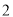 B.
B. 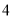 C.
C. 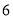 D.
D. 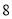
查看答案和解析>>
科目:初中数学 来源:2017年广西防城港市中考数学模拟试卷 题型:解答题
一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
(1)16种等可能的结果数,它们是:11,41,71,81,14,44,74,84,17,47,77,87,18,48,78,88;(2) 【解析】(1)画树状图: 共有16种等可能的结果数,它们是:11,41,71,81,14,44,74,84,17,47,77,87,18,48,78,88; (2)算术平方根大于4且小于7的结果数为6, 所以算术平方根大于4且小于7的概...查看答案和解析>>
科目:初中数学 来源:2017年广西防城港市中考数学模拟试卷 题型:填空题
函数y=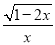 的自变量x的取值范围是_____.
的自变量x的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:填空题
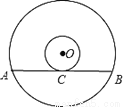
如图,是一张电脑光盘的表面,两个圆心都是O,大圆的弦AB所在的直线是小圆的切线,切点为C,已知大圆的半径为5cm,小圆的半径为1cm,则弦AB的长是 .
查看答案和解析>>
科目:初中数学 来源:安徽省芜湖市教育集团2017-2018学年度上学期八年级第二次月考 题型:单选题
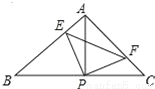
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③△PEF是等腰直角三角形,④当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),S四边形AEPF=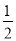 S△ABC,上述结论中始终正确有 ( )
S△ABC,上述结论中始终正确有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】∵AB=AC,∠BAC=90°,P是BC中点, ∴AP⊥BC,AP=PB, ∠B=∠CAP=45°, ∵∠APF+∠FPA=90°, ∠ APF+∠BPE=90°, ∴∠APF=∠BPE, 在△BPE和△APF中, ∠B=∠CAP, BP=AP,∠BPE =∠APF, ∴△PFA≌△PEB;故①正确; ∵△ABC是等腰直角三角...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com