
过多边形的一个顶点可以作7条对角线,则此多边形的内角和是外角和的( )
A. 4倍 B. 5倍 C. 6倍 D. 3倍
A 【解析】∵过多边形的一个顶点共有7条对角线, ∴该多边形边数为10, ∴(10﹣2)•180°=1440°, ∴这个多边形的内角和为1440°, 又∵多边形的外角和为360°, ∴1440÷360=4. 故选A.科目:初中数学 来源:2018人教版七年级数学下册练习:第六章达标检测卷 题型:单选题
下列说法:①一个数的平方根一定有两个;②一个正数的平方根一定是它的算术平方根;③负数没有立方根.其中正确的个数有( )
A. 0个 B. 1个 C. 2个 D. 3个
A 【解析】∵负数没有平方根,故错误;②∵一个正数的正的平方根一定是它的算术平方根,故错误;③∵负数有一个负的立方根,故错误. 故选A.查看答案和解析>>
科目:初中数学 来源:湖北省鄂州市2017-2018学年七年级(上)期中数学试卷 题型:填空题
多项式x3﹣5xy2﹣7y3+8x2y按x的降幂排列为______.
x3+8x2y﹣5xy2﹣7y3. 【解析】多项式x3﹣5xy2﹣7y3+8x2y的各项为x3、﹣5xy2、﹣7y3、8x2y,按x的降幂排列为:x3+8x2y﹣5xy2﹣7y3.查看答案和解析>>
科目:初中数学 来源:甘肃省平凉市2017-2018学年八年级(上)期中数学试卷 题型:解答题
如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.

查看答案和解析>>
科目:初中数学 来源:甘肃省平凉市2017-2018学年八年级(上)期中数学试卷 题型:填空题
如图,△ABD≌△BAC,若AD=BC,则∠BAD的对应角是______.
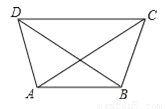
查看答案和解析>>
科目:初中数学 来源:甘肃省平凉市2017-2018学年八年级(上)期中数学试卷 题型:单选题
在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1: 2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】①因为∠A+∠B=∠C,则2∠C=180°,∠C=90°,所以△ABC是直角三角形; ②因为∠A:∠B:∠C=1:2:3,设∠A=x,则x+2x+3x=180,x=30°,∠C=30°×3=90°,所以△ABC是直角三角形; ③因为∠A=90°?∠B,所以∠A+∠B=90°,则∠C=180°?90°=90°,所以△ABC是直角三角形; ④因为3∠A=2∠B=∠C...查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学人教版上册:第24章 圆 单元测试卷 题型:解答题
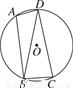
如图,已知四边形ABCD内接于圆O,连接BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求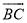 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学人教版上册:第24章 圆 单元测试卷 题型:单选题
如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )
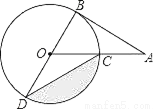
A. 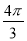 ﹣
﹣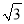 B.
B. 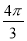 ﹣2
﹣2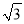 C. π﹣
C. π﹣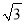 D.
D. 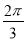 ﹣
﹣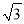
查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学人教版上册:第23章 旋转 单元测试卷 题型:填空题
如图,将△OAB绕点O逆时针连续旋转两次得到△OA″B″,每次旋转的角度都是50°,若∠B″OA=124°,则∠AOB=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com