
以下列各组数据为边长作三角形,其中能组成直角三角形的是( ).
A. 3,5,3 B. 4,6,8 C. 7,24,25 D. 6,12,13
C 【解析】试题分析:欲求证是否为直角三角形,这里给出三边的长,只要满足勾股定理的逆定理即可.A、;B、;C、;D、.根据勾股定理7,24,25能组成直角三角形. 故选:C. 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源:人教版九年级上册数学 第25章小结与复习 测试 题型:单选题
(德州中考)经过某十字路口的汽车,可能直行,也可能左转或者右转.如果这三种可能性大小相同,则经过这个十字路口的两辆汽车一辆左转,一辆右转的概率是( )
A. 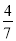 B.
B. 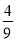 C.
C. 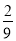 D.
D. 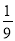
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:解答题
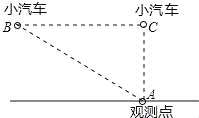
“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:单选题
三角形的三边长满足关系:(a+b)2=c2+2ab,则这个三角形是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形
B 【解析】 试题分析:根据已知条件可得:+2ab=+2ab,则=,则这个三角形就是直角三角形.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:单选题
如图,△ABD和△BCE都是等腰直角三角形,如果CD=17,BE=5,那么AC的长为( )
A. 13 B. 12 C. 7 D. 5
A 【解析】试题分析:根据已知条件可得:BC=BE=5,则AB=DB=17-5=12,根据三角形三边关系可得:12-5<AC<12+5 即7<AC<17,根据直角三角形的性质可得:AC>AB=12,即12<AC<17.查看答案和解析>>
科目:初中数学 来源:北师大版九年级上册4.7三角形相似专题--高的比等于相似比 题型:单选题
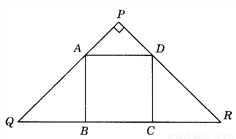
如图,正方形ABCD的边BC在等腰直角三角形PQR的底边QR上,其余两个顶点A、D分别在PQ、PR上,则PA∶AQ=( ).
A. 1∶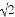 B. 1∶2 C. 1∶3 D. 2∶3
B. 1∶2 C. 1∶3 D. 2∶3
查看答案和解析>>
科目:初中数学 来源:广东省2017届九年级上学期第二次月考数学试卷 题型:解答题
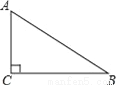
如图,在Rt△ABC中,∠C=90°.
(1)用直尺和圆规作△ABC的BC边上的垂直平分线,与AB交于D点,与BC交于E点(保留作图痕迹,不写作法);
(2)若AC=6,AB=10,连结CD,求DE,CD的长.
查看答案和解析>>
科目:初中数学 来源:广东省2017届九年级上学期第二次月考数学试卷 题型:单选题
如果关于x的一元二次方程x2+px+q=0的两根分别为x1=2,x2=1,那么p,q的值分别是( )
A. ﹣3,2 B. 3,﹣2 C. 2,﹣3 D. 2,3
A 【解析】析:根据根与系数的关系,即可求得p、q的值. 【解析】 由题意,得:x1+x2=-p,x1x2=q; ∴p=-(x1+x2)=-3,q=x1x2=2; 故选A.查看答案和解析>>
科目:初中数学 来源:《概率的进一步认识》单元测试2 题型:填空题
某射手在同一条件下进行射击,结果如下表所示:
射击次数(n) | 10 | 20 | 50 | 100 | 200 | 500 | … |
击中靶心次数(m) | 8 | 19 | 44 | 92 | 178 | 455 | … |
击中靶心频率( | … |
请填好最后一行的各个频率,由此表推断这个射手射击1次,击中靶心的概率的是___________.
0.8,0.95,0.88,0.92,0.89,0.91,0.9 【解析】 射击次数(n) 10 20 50 100 200 500 … 击中靶心次数(m) 8 19 44 92 178 455 … 击中靶心频率() 0.8 0.95 0.88 0.92 0.8...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com