
��ͼ��������ABCD�ı�BC�ڵ���ֱ��������PQR�ĵױ�QR�ϣ�������������A��D�ֱ���PQ��PR�ϣ���PA��AQ����������
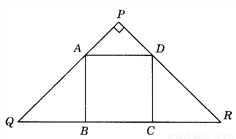
A. 1��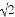 B. 1��2 C. 1��3 D. 2��3
B. 1��2 C. 1��3 D. 2��3

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ����һ��ѧ��һѧ��5.2.3ȥ��ĸ��һԪһ�η��� ͬ����ϰ ���ͣ������
�ⷽ�̣� 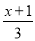 +1=x��
+1=x��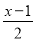 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ��ȱ�����ѧ��ʦ�����꼶��ѧ�ϲ� ��һ�� ���ɶ��� ����� ���ͣ������
��ͼ����֪�ı���ABCD�У���B=90�㣬AB=3��BC=4��CD=12��AD=13�����ı���ABCD�������
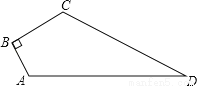
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ��ȱ�����ѧ��ʦ�����꼶��ѧ�ϲ� ��һ�� ���ɶ��� ����� ���ͣ���ѡ��
��֪��ABC�����߷ֱ�Ϊ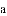
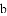
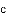
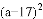 ��
��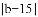 +
+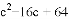 ��0�����ABC�ǣ� ����
��0�����ABC�ǣ� ����
A. ��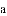
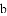
C. ��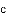
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ��ȱ�����ѧ��ʦ�����꼶��ѧ�ϲ� ��һ�� ���ɶ��� ����� ���ͣ���ѡ��
�����и�������Ϊ�߳��������Σ����������ֱ�������ε��ǣ� ��.
A. 3��5��3 B. 4��6��8 C. 7��24��25 D. 6��12��13
C ���������������������֤�Ƿ�Ϊֱ�������Σ�����������ߵij���ֻҪ���㹴�ɶ������涨�����ɣ�A����B����C����D�������ݹ��ɶ���7��24��25�����ֱ��������. ��ѡ��C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ2017����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
������ij¥������ÿƽ����6000Ԫ�ľ��۶������ۣ����ڹ���Ժ�йط��ز��������߳�̨�����ֱ߳ҹ��������ز�������Ϊ�˼ӿ��ʽ���ת���Լ۸������µ�������ÿƽ����4860Ԫ�ľ��ۿ������ۣ�
��1����ƽ��ÿ���µ��İٷ��ʣ�
��2��ij�����Կ��̼۾��۹���һ��100ƽ����ס���������̸������������Żݷ����Թ�ѡ��
�ٴ�9.8�����ۣ�
�ڲ����ۣ�һ������װ��ÿƽ����80Ԫ���������ַ������Żݣ�
��1��ƽ��ÿ���µ��İٷ���Ϊ10%����2�������ٸ��Żݣ� �������������������1��������������г���Ӧ�ķ��̣��Ӷ��������ƽ��ÿ���µ��İٷ��ʣ� ��2������������Էֱ��������ַ����µ��Żݶ�ȣ��Ӷ����Խ���⣮ ��������� ��1����ƽ��ÿ���µ��İٷ���Ϊx���� 6000��1-x��2=4860 ��ã�x1=0.1�� x2=1.9���������⣬��ȥ�� ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ2017����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
���κ���y=x2��2x+6����Сֵ��____��
5 �����������������y=x2��2x+6=x2��2x+1+5 =��x��1��2+5�� �ɼ������κ�������СֵΪ5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ ��24��С���븴ϰ ��ϰ ���ͣ������
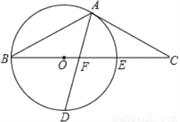
��ͼ���ԡ�ABC��BC����һ��OΪԲ�ĵ�Բ������A��B���㣬����BC�߽��ڵ�E��DΪBE���°�Բ�����е㣬����AD��BC��F��AC=FC��
��1����֤��AC�ǡ�O�����ߣ�
��2����֪Բ�İ뾶R=5��EF=3����DF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������ʵĽ�һ����ʶ����Ԫ����2 ���ͣ������
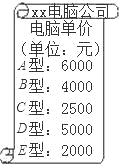
ij���Թ�˾����A��B��C�����ͺŵļ�Ʒ�Ƶ��Ժ�D��E�����ͺŵ���Ʒ�Ƶ��ԣ�ϣ����ѧҪ�Ӽס�������Ʒ�Ƶ����и�ѡ��һ���ͺŵĵ��ԣ�
��1��д������ѡ��������������״ͼ���б�������ʾ����
��2�������1���и���ѡ��������ѡ�еĿ�������ͬ����ôA�ͺŵ��Ա�ѡ�еĸ����Ƕ��٣�
��3����֪ϣ����ѧ����ס�������Ʒ�Ƶ��Թ�36̨���۸���ͼ��ʾ����ǡ������10��Ԫ����ң����м�Ʒ�Ƶ���ΪA�ͺŵ��ԣ������A�ͺŵ����м�̨��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com