
已知数串:  依照这前15个数的分子、分母的构成规律排列下去,第100个数是( )
依照这前15个数的分子、分母的构成规律排列下去,第100个数是( )
A. 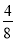 B.
B.  C.
C. 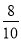 D.
D. 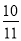
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源:2017年湖北省黄冈市中考数学三模试卷 题型:单选题
下列命题中错误的命题是( )
A. 直径所对的圆周角是直角
B. 圆既是轴对称图形,又是中心对称图形
C. 三点确定一个圆
D. 在同圆中,相等的圆周角所对的弦相等
C 【解析】试题解析:A、根据圆周角定理,故本选项正确,不符合题意; B、根据轴对称图形和中心对称图形的定义,故本选项正确,不符合题意; C、当三点在同一直线上时,不能确定一个圆,故本选项错误,符合题意; D、根据圆周角定理,故本选项正确,不符合题意. 故选C.查看答案和解析>>
科目:初中数学 来源:2017广东省深圳市中考数学模拟试卷(三) 题型:填空题
在﹣42,+0.01,π,0,120,这5个数中正有理数是________.
+0.01,120 【解析】正有理数有+0.01,120(其中π是无理数,所以不能选).查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西省七年级(下)第二次测验数学试卷 题型:解答题
列方程解应用题
甲、乙两人同时从相距25千米的A地去B地,甲骑车乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40分钟,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好3小时,求两人的速度各是多少?
甲的速度为15千米/小时,乙的速度为5千米/小时. 【解析】试题分析:可设乙的速度为x千米/小时,则甲的速度为3x千米/小时,根据关于路程的等量关系:甲、乙两人行驶的路程和是两个25千米,列出方程求解即可. 【解析】 设乙的速度为x千米/小时,则甲的速度为3x千米/小时,依题意有 3x(3﹣)+3x=25×2, 9x﹣2x+3x=50, 10x=50, x=5...查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西省七年级(下)第二次测验数学试卷 题型:填空题
方程(a-2)x|a|-1+3=0是关于x的一元一次方程,则a=____.
-2 【解析】试题解析:根据一元一次方程的定义,可得: 解得: 把代入方程得: 解得: 故答案为:查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西省七年级(下)第二次测验数学试卷 题型:单选题
下列说法中正确的是( )
A. 两条射线组成的图形叫做角
B. 小于平角的角可分为锐角和钝角两类
C. 射线就是直线
D. 两点之间的所有连线中,线段最短
D 【解析】根据真假命题的概念,可知: A、有公共端点的两条射线组成的图形叫做角,选项错误; B、小于平角的角可分为锐角、钝角,还应包含直角,选项错误. C、射线是直线的一部分,选项错误; D、两点之间的所有连线中,线段最短,选项正确; 故选:D.查看答案和解析>>
科目:初中数学 来源:江苏省徐州市丰县2017-2018学年八年级上学期第二次月考数学试卷 题型:解答题
如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8,设CD=x.
(1)用含x的代数式表示AC+CE的长.
(2)请问点C满足什么条件时,AC+CE的值最小?并求出最小值;
(3)根据(2)中的规律和结论,请构图求出代数式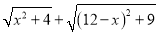 的最小值.
的最小值.
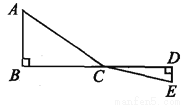
查看答案和解析>>
科目:初中数学 来源:安徽省16-17学年度第一学期七年级数学期末考试卷 题型:解答题
老师在黑板上写了一个正确的演算过程,随后用手掌捂住了多项式,形式如下:
-(a2+4ab+4b2)=a2-4b2
(1)求所捂的多项式;
(2)当a=-1,b=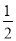 时求所捂的多项式的值.
时求所捂的多项式的值.
查看答案和解析>>
科目:初中数学 来源:山西农业大学附属中学2017-2018学年八年级上学期第三次月考数学试卷 题型:单选题
设一个正方形的边长为acm,若边长增加3cm,则新正方形的面积增加了
A. 9cm2 B. 6acm2 C. (6a+9)cm2 D. 无法确定
C 【解析】根据题意列得:(a+3)²?a²=a²+6a+9?a²=(6a+9)平方厘米 则新正方形的面积增加了(6a+9)平方厘米. 故选C查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com