
下面是小林做的4道作业题:(1)2ab+3ab=5ab;(2)2ab﹣3ab=﹣ab;(3)2ab﹣3ab=6ab;(4)2ab÷3ab=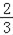 .做对一题得2分,则他共得到( )
.做对一题得2分,则他共得到( )
A. 2分 B. 4分 C. 6分 D. 8分
C 【解析】(1)2ab+3ab=5ab,正确; (2)2ab﹣3ab=﹣ab,正确; (3)∵2ab﹣3ab=﹣ab,∴2ab﹣3ab=6ab错误; (4)2ab÷3ab=,正确.3道正确,得到6分, 故选项C正确. 故选:C.科目:初中数学 来源:辽宁省2017-2018学年八年级上学期期末模拟数学试卷 题型:单选题
下列图案中,轴对称图形是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:单选题
某农户买黄金瓜,第一天上午买了45斤,价格为每斤x元,下午他又买了35斤,价格为每斤y元.第二天他以每斤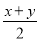 元的价格卖完了80斤,结果同第一天比发现自己亏了.其原因是( )
元的价格卖完了80斤,结果同第一天比发现自己亏了.其原因是( )
A. x<y B. x>y C. x≤y D. x≥y
B 【解析】【解析】 根据题意,可得:买黄瓜每斤的平均价>卖黄瓜每斤的平均价,∴(45x+35y)÷(45+35)>,∴(45x+35y)÷80>,∴(45x+35y)÷80×80>×80,∴45x+35y>40x+40y,整理,可得:x>y.故选B.查看答案和解析>>
科目:初中数学 来源:2017年山东省中考数学二模试卷 题型:解答题
某中学为促进课堂教学,提高教学质量,对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查.根据收回的问卷,学校绘制了如下图表,请你根据图表中提供的信息,解答下列问题.
编号 | 教学方式 | 最喜欢的频数 | 频率 |
1 | 教师讲,学生听 | 20 | 0.10 |
2 | 教师提出问题,学生探索思考 | ||
3 | 学生自行阅读教材,独立思考 | 30 | |
4 | 分组讨论,解决问题 | 0.25 |
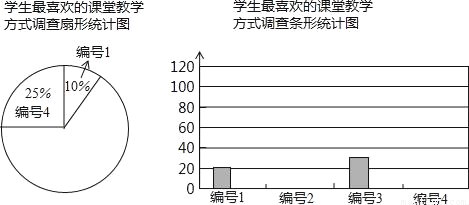
(1)收回的问卷份数为 ,把条形统计图补充完整;
(2)扇形统计图中编号1与编号4的圆心角分别是多少度?
(3)你最喜欢以上哪一种教学方式,请提出你的建议,并简要说明理由.
(1)200,补图见解析;(2)编号1的圆心角是36°,编号4的圆心角是90°;(3)答案见解析. 【解析】试题分析:(1)根据编号1的数量及其百分比可得总人数,总人数乘以编号4的百分比求得其人数,总人数减去其他编号的数量求得编号2的人数,即可补全条形图; (2)用360°乘以其所占百分比即可得; (3)根据条形图各编号的具体人数,提出合理的建议均可. 试题解析:(1)收回...查看答案和解析>>
科目:初中数学 来源:2017年山东省中考数学二模试卷 题型:单选题
已知AC⊥BC于C,BC=a,CA=b,AB=c,下列选项中⊙O的半径为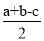 的是( )
的是( )
A. 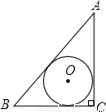 B.
B. 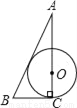 C.
C. 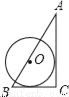 D.
D. 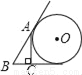
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
如图所示,梯形AOCD中,AD=9,OC=10,AO=4,在线段OC上任取一点N(不与O,C重合),连接DN,作NE⊥DN,交AO于点E.
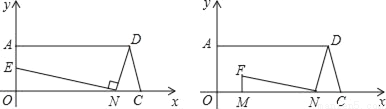
(1)当CN=2时,求点E的坐标.
(2)若CN=x,OE=y,求y与x的函数关系式.
(3)探索与研究:若点M从O点沿OC方向、N点从C点沿CO方向同时等速运动,现有一点F,满足MF⊥MN,NF⊥ND.
①猜想F点在什么线上运动?并求出这条线所对应的函数关系式,并写出自变量的取值范围;
②求出F点在运动过程中的最高点的坐标.
(1)点E的坐标为(0,2);(2)①当0<x<1时,y=;②当x>1时,y=;(3)①y=﹣x2+3x﹣(0<x<10);②最高点的坐标是(3,2). 【解析】试题分析: 试题解析:(1)如图所示,作DF⊥OC于F, 由题意知,CN=2,AD=9,OC=10. ∵AOCD是梯形且 ∴OF=AD=9,CF=OC?OF=1,NF=CN?CF=1,DF=OA=4. ...查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
如图所示,直线y=﹣2x+8与两坐标轴分别交于P、Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.若矩形ABOC的面积为5,求点A坐标.
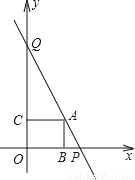
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学三模试卷 题型:单选题
已知两圆的直径分别为7和1,当它们相切时,圆心距为( )
A. 8 B. 6 C. 8或6 D. 4或3
D 【解析】试题解析:∵直径分别为7和1, ∴两圆半径分别为3.5和0.5, ∴当两圆外切时,圆心距为3.5+10.5=4; 当两圆内切时,圆心距为3.5?0.5=3. 故选D.查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷 题型:填空题
如图,在平面直角坐标系中,抛物线y=﹣x2+4x与x轴交于点A,点M是x轴上方抛物线上一点,过点M作MP⊥x轴于点P,以MP为对角线作矩形MNPQ,连结NQ,则对角线NQ的最大值为_____.
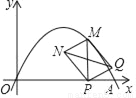
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com