
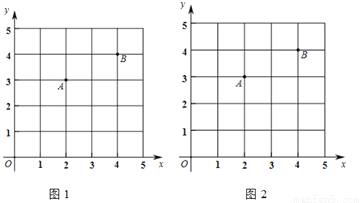
在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画出所有符合条件的整点三角形.
(1)在图1中画△PAB,使点P的横、纵坐标之和等于点A的横坐标;
(2)在图2中画△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.
科目:初中数学 来源:2017年河北省沧州市中考数学模拟试卷(六) 题型:填空题
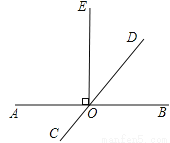
如图,直线AB、CD相交于点O,OE⊥AB,垂足为O,如果∠EOD=42°,则∠AOC=______度.
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级12月月考数学试卷 题型:解答题
解方程: 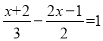 .
.
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级12月月考数学试卷 题型:单选题
已知代数式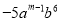 和
和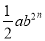 是同类项,则
是同类项,则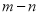 的值是( )
的值是( )
A. 1 B. -1 C. -2 D. -3
B 【解析】试题分析:根据同类项的定义的两个条件:所含字母相同,相同字母的指数相同 所以m-1=1, 2n=6, m=2,n=3可得m-n="2=3=-1," 所以选B.查看答案和解析>>
科目:初中数学 来源:江苏省高邮市2017-2018学年八年级12月月考数学试卷 题型:解答题
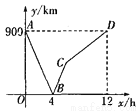
列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km).图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
(1)甲、乙两地之间的距离为_________km;
(2)求慢车和快车的速度;
(3)请解释图中点C的实际意义;
(4)分别写出线段AB、BC所表示的y与x之间的函数关系式;
(5)在整个行驶过程中,两车何时相距25km,请求出相应的x的值.
查看答案和解析>>
科目:初中数学 来源:江苏省高邮市2017-2018学年八年级12月月考数学试卷 题型:填空题
九年级某班有48名学生,所在教室有6行8列座位,用(m,n)表示第m行第n列的座位,新学期准备调整座位.设某个学生原来的座位为(m,n),若调整后的座位为(i,j),则称该生作了平移[a,b]=[m-i,n-j],并称a+b为该生的位置数.若某生的位置数为9,则当m+n取最小值时,m·n的最大值为_______.
30 【解析】由题意得a+b=m-i+n-j=9, 则m+n=9+(i+j), ∵m、n、i、j表示行数与列数, ∴当i=j=1时,m+n取最小值11, 此时n=11-m, ∴m•n=m(11-m), 又m=1,2,3,4,5,6. 则m=1时,m•n=10;m=2时,m•n=18;m=3时,m•n=24;m=4时,m•n=28;m=5时,m•n=30;...查看答案和解析>>
科目:初中数学 来源:江苏省高邮市2017-2018学年八年级12月月考数学试卷 题型:填空题
若实数m,n满足(m+1)2+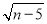 =0,则
=0,则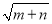 =__.
=__.
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市西湖区绿城育华2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
如图,是一张长方形纸片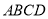 ,已知
,已知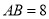 ,
, 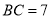 ,
, 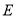 为边
为边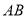 上一点,
上一点, 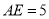 ,现在要剪下一张等腰三角形纸片(
,现在要剪下一张等腰三角形纸片(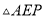 ),要使点
),要使点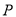 落在长方形
落在长方形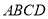 的某一边上,则
的某一边上,则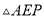 的底边长为__________.
的底边长为__________.

查看答案和解析>>
科目:初中数学 来源:河南省邓州市2018届九年级上学期期中质量评估---数学试卷word版 题型:解答题
某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5 000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5 000元.
(1)当每间商铺的年租金定为13万元时,能租出多少间?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)为284万元?
(1)24;(2)每间商铺的年租金定为13.5万元或12万元. 【解析】试题分析:(1)租金增加30000元,少租出6间,故可租出24间; (2)设每间商铺的年租金增加x万元,根据:租金﹣各种费用=收益,列方程求解. 试题解析:【解析】 (1)∵30﹣(130000﹣100000)÷5000=30﹣6=24,∴能租出24间; 【解析】 (1)30-=24(间) (...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com