
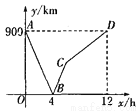
列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km).图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
(1)甲、乙两地之间的距离为_________km;
(2)求慢车和快车的速度;
(3)请解释图中点C的实际意义;
(4)分别写出线段AB、BC所表示的y与x之间的函数关系式;
(5)在整个行驶过程中,两车何时相距25km,请求出相应的x的值.
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源:2017年河北省沧州市中考数学模拟试卷(六) 题型:解答题
先化简,再求值: 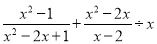 ,其中x=
,其中x=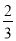 .
.
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级12月月考数学试卷 题型:解答题
已知数轴上三点M,O,N对应的数分别为-3,0,1,点P为数轴上任意一点,其对应的数为x.
(1)如果点P到点M,点N的距离相等,那么x的值是______________;
(2)数轴上是否存在点P,使点P到点M,点N的距离之和是5?若存在,请直接写出x的值;若不存在,请说明理由.
(1)-1;(2 )存在符合题意的点P,此时x=-3.5或1.5. 【解析】试题分析:(1)根据三点M,O,N对应的数,得出NM的中点为:x=(-3+1) ÷2进而求出即可; (2)根据P点在N点右侧或在M点左侧分别求出即可. 【解析】 (1)-1. (2 )存在符合题意的点P,此时或. 解:(1),O,N对应的数分别为-3,0,1,点P到点M,点N的距离相等, ...查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级12月月考数学试卷 题型:填空题
-2的倒数是_________.
【解析】∵乘积为1的两个数互为倒数, ∴-2的倒数是 .查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级12月月考数学试卷 题型:单选题
把弯曲的河道改直,能够缩短船舶航行的路程,这样做的道理是( )
A. 垂线段最短 B. 两点确定一条直线
C. 两点之间,直线最短 D. 两点之间,线段最短
D 【解析】把弯曲的河道改直,能够缩短船舶航行的路程,这样做的道理是两点之间,线段最短. 故选D.查看答案和解析>>
科目:初中数学 来源:江苏省高邮市2017-2018学年八年级12月月考数学试卷 题型:解答题
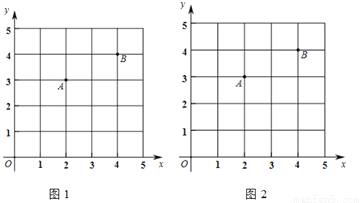
在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画出所有符合条件的整点三角形.
(1)在图1中画△PAB,使点P的横、纵坐标之和等于点A的横坐标;
(2)在图2中画△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.
查看答案和解析>>
科目:初中数学 来源:江苏省高邮市2017-2018学年八年级12月月考数学试卷 题型:填空题
已知一次函数y=ax+b,且2a+b=1,则该一次函数图象必经过点_________.
(2,1) 【解析】∵一次函数y=ax+b, ∴当x=2,y=2a+b, 又2a+b=1, ∴当x=2,y=1, 即该图象一定经过点(2,1). 故答案为(2,1).查看答案和解析>>
科目:初中数学 来源:浙江省杭州市西湖区绿城育华2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
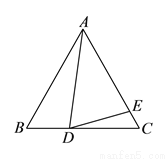
已知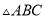 ,
, 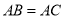 ,
, 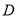 为
为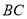 上一点,
上一点, 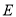 为
为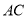 上一点,
上一点, 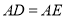 .
.
( )如果
)如果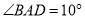 ,
, 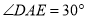 ,那么
,那么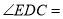 __________
__________ .
.
(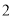 )如果
)如果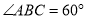 ,
, 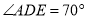 ,那么
,那么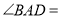 __________
__________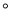 ,
, 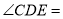 __________
__________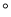 .
.
(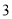 )设
)设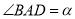 ,
, 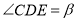 猜想
猜想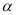 ,
, 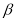 之间的关系式,并说明理由.
之间的关系式,并说明理由.
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市余杭区英特外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
下列四组条件中,能够判定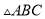 和
和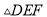 全等的是( ).
全等的是( ).
A. 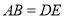 ,
, 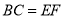 ,
, 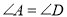 B.
B. 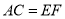 ,
, 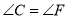 ,
, 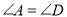
C. 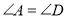 ,
, 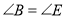 ,
, 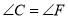 D.
D. 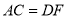 ,
, 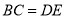 ,
, 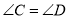
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com