练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，BF=EC，∠B=∠E，请问添加下面哪个条件不能判断△ABC≌△DEF（　 ）

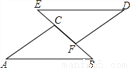
    A. ∠A=∠D B. AB=ED C. DF∥AC D. AC=DF

    D 【解析】试题分析：A、添加∠A=∠D，可用AAS判定△ABC≌△DEF． B、添加AB=ED，可用SAS判定△ABC≌△DEF； C、添加DF∥AC，可证得∠C=∠F，用AAS判定△ABC≌△DEF； D、添加AC=DF，SSA不能判定△ABC≌△DEF． 故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省2017-2018学年度上期九年级数学第三次月考试卷 题型：解答题

    已知关于x的一元二次方程x2－mx－2＝0…①.

    （1）对于任意的实数m,判断方程①的根的情况,并说明理由．

    （2）若x＝－1是这个方程的一个根，求m的值和方程①的另一根．

    (1)见解析；(2) x＝2. 【解析】试题分析： 利用一元二次方程根的情况可以转化为判别式△与0的关系进行判断． 直接把代入方程即可求得的值，然后解方程即可求得方程的另一个根； 试题解析：(1) 因为对于任意实数， 所以所以对于任意的实数，方程有两个不相等的实数根． (2)因为是方程的一个根， 所以 解得 方程为 解得 所以方程的另一根为

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东钱湖九校2017-2018学年七年级上册数学期中联考试卷 题型：单选题

    单项式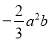的（      ）

    A. 系数是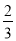，次数是2次 B. 系数是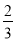，次数是3次

    C. 系数是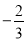，次数是2次 D. 系数是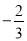，次数是3次

    D 【解析】试题解析：单项式的系数是： 次数是： 故选D.

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2016-2017学年八年级上学期期末考试数学试卷 题型：填空题

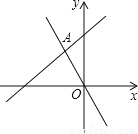
    如图，函数y=﹣2x和y=kx+b的图象相交于点A（m，3），则关于x的不等式kx+b+2x＞0的解集为 ．

    x＞﹣． 【解析】 试题分析：首先将点A的坐标代入正比例函数中求得m的值，然后结合图象直接写出不等式的解集即可． 试题解析：∵函数y=﹣2x经过点A（m，3）， ∴﹣2m=3， 解得：m=﹣， 则关于x的不等式kx+b+2x＞0可以变形为kx+b＞﹣2x， 由图象得：kx+b＞﹣2x的解集为x＞﹣．

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2016-2017学年八年级上学期期末考试数学试卷 题型：单选题

    在平面直角坐标系中，直线与x轴、y轴分别交于A、B两点，点O为坐标原点，若在该坐标平面内有以点P（不与点A、B、O重合）为顶点的直角三角形与Rt△ABO全等，且这个以点P为顶点的直角三角形与Rt△ABO有一条公共边，则所有符合条件的P点个数为（　　）

    A. 9个 B. 7个 C. 5个 D. 3个

    B 【解析】【解析】 如图，图中的P1、P2、P3、P4、P5、P6、P7，就是符合要求的点P，注意以P1为公共点的直角三角形有3个．故选B．

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年八年级上学期第二次统测数学试卷 题型：解答题

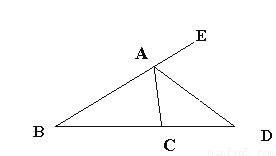
    如图，AD是⊿ABC的外角平分线，交BC的延长线于D点，若∠B = 30º，∠DAE = 55º，求∠ACD的度数。

    100°． 【解析】试题分析：根据角平分线的定义得出∠CAE的度数，再由三角形外角的性质得出∠ACB的度数，根据平角的定义即可得出结论． 试题解析：【解析】 ∵∠DAE=55°，ADF平分∠CAE， ∴∠CAE=110°， ∵∠CAE是△ABC的外角，∠B=30°， ∴∠ACB=110°-30°=80°， ∴∠ACD=180°-80°=100°．

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年八年级上学期第二次统测数学试卷 题型：填空题

    观察下列各式，探索发现规律：

    22－1＝3＝1×3；42－1＝15＝3×5；62－1＝35＝5×7；82－1＝63＝7×9；102－1＝99＝9×11；……用含n的式子表示第n个式子为_____________.

    【解析】等式的左边为相应序号位置的偶数的平方与1的差，右边为相邻两个奇数的积，这两个奇数与偶数是连续的三个整数，即： 左边：（2n）2-1， 右边：（2n-1）（2n+1）， ∴规律为（2n）2-1=（2n-1）（2n+1）， 故答案为：（2n）2-1=（2n-1）（2n+1）.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（华师大版）：期末检测1 题型：解答题

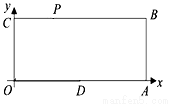
    已知：如图，O为坐标原点，四边形OABC为矩形，A(10，0)，C(0，4)，点D是OA的中点，点P在BC上以每秒1个单位的速度由C向B运动。

    (1) 求梯形ODPC的面积S与时间t的函数关系式。

    (2) t为何值时，四边形PODB是平行四边形？

    (3) 在线段PB上是否存在一点Q，使得ODQP为菱形。若存在求t值，若不存在，说明理由。

    (4) 当△OPD为等腰三角形时，求点P的坐标。

    （1）由题意仪，根据梯形的面积公式，得 s==2t+10 （2）∵四边形PODB是平行四边形， ∴PB=OD=5， ∴PC=5， ∴t=5 （3）∵ODQP为菱形， ∴OD=OP=PQ=5， ∴在Rt△OPC中，由勾股定理得： PC=3 ∴t=3 （4）当P1O=OD=5时，由勾股定理可以求得P1C=3， P2O=P2D时，作...

    查看答案和解析>>

    科目：初中数学 来源：广东省2018届九年级上学期学业检测（二）数学试卷 题型：单选题

    若关于x的一元二次方程（k﹣1）x2+2x﹣2=0有两个不相等的实数根，则k的取值范围是（　　）

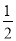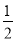    A. k＞ B. k≥ C. k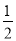＞且k≠1 D. k≥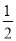且k≠1

    C 【解析】试题分析：根据题意得k-1≠0且△=2²-4（k-1）×（-2）＞0，解得：k＞且k≠1．故选C

    查看答案和解析>>

    同步练习册答案