练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

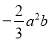    单项式的（      ）

    A. 系数是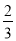，次数是2次 B. 系数是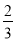，次数是3次

    C. 系数是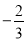，次数是2次 D. 系数是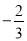，次数是3次

    D 【解析】试题解析：单项式的系数是： 次数是： 故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省2017-2018学年八年级上学期第二次月考数学试卷 题型：解答题

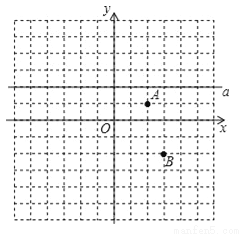
    如图，已知点A，B（3，﹣2）在平面直角坐标系中，按要求完成下列个小题．

    （1）写出与点A关于y轴对称的点C的坐标，并在图中描出点C；

    （2）在（1）的基础上，点B，C表示的是两个村庄，直线a表示河流，现要在河流a上的某点M处修建一个水泵站，向B、C两个村庄供水，并且使得管道BM+CM的长度最短，请你在图中画出水泵站M的位置．

    （1）作图见解析，C（－2，1）；（2）答案见解析． 【解析】试题分析：（1）根据轴对称与平面直角坐标系的关系，直接求解即可； （2）根据“两点之间，线段最短”，由轴对称的性质求解即可. 试题解析：（1）点A关于y轴对称的点C的坐标为（-2，1），标注在图形上为： （2）①作点B关于直线a的对称点B′, ②连接CB′与直线a的交点为M， 点M求是所求的点.（理由...

    查看答案和解析>>

    科目：初中数学 来源：江苏省2017-2018学年度上期九年级数学第三次月考试卷 题型：填空题

    抛物线y=x2﹣2x+1的顶点坐标是______．

    （1，0） 【解析】试题解析：∵y=x2-2x+1=（x-1）2， ∴抛物线顶点坐标为（1，0）．

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东钱湖九校2017-2018学年七年级上册数学期中联考试卷 题型：填空题

    为鼓励节约用电，某地对居民用电收费标准作如下规定：每户每月用电如果不超过100度，那么每度电价按a元收费；如果超过100度，那么超过部分每度电价按b元收费，某户居民在一个月内用电160度，该户居民这个月应缴纳电费是_________元（用含a、b的代数式表示）．

    （100a+60b） 【解析】因为160＞100，所以其中100度是每度电价按a元收费，多出来的60度是每度电价按b元收费． 【解析】 100a+（160-100）b=100a+60b． 故答案为：（100a+60b）． 该题要分析清题意，要知道其中100度是每度电价按a元收费，多出来的60度是每度电价按b元收费． 用字母表示数时，要注意写法： ①在代数式中出...

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东钱湖九校2017-2018学年七年级上册数学期中联考试卷 题型：单选题

    正方形ABCD在数轴上的位置如图所示，点D、A对应的数分别为0和1，若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为2；则翻转2017次后，数轴上数2017所对应的点是 （ ）

    A. 点A B. 点B C. 点C D. 点D

    A 【解析】试题解析： 当正方形在转动第一周的过程中，1所对应的点是A，2所对应的点是B，3所对应的点是C，4所对应的点是D， ∴四次一循环， ∵2017÷4=504…1， ∴2017所对应的点是A， 故选A.

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2016-2017学年八年级上学期期末考试数学试卷 题型：解答题

    如图，直线AB交x轴正半轴于点A（a，0），交y轴正半轴于点B（0，b），且a、b满足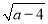+|4-b|=0，

    （1）求A、B两点的坐标；

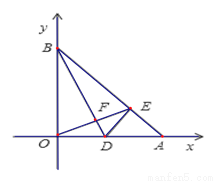
    （2）D为OA的中点，连接BD，过点O作OE⊥BD于F，交AB于E，求证:∠BDO=∠EDA；

    （3）如图，P为x轴上A点右侧任意一点，以BP为边作等腰Rt△PBM，其中PB=PM，直线MA交y轴于点Q，当点P在x轴上运动时，线段OQ的长是否发生变化？若不变，求其值；若变化，求线段OQ的取值范围．

    （1）A（4，0），B（0，4）（2）证明见解析（3）无论P点怎么动OQ的长不变 【解析】试题分析：（1）首先根据已知条件和非负数的性质得到关于a、b的方程，解方程组即可求出a，b的值，也就能写出A，B的坐标； （2）作出∠AOB的平分线，通过证△BOG≌△OAE得到其对应角相等解决问题； （3）过M作x轴的垂线，通过证明△PBO≌△MPN得出MN=AN，转化到等腰直角三角形中去...

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2016-2017学年八年级上学期期末考试数学试卷 题型：解答题

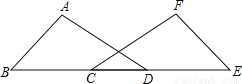
    如图，在△ABD和△FEC中，点B，C，D，E在同一直线上，且AB =FE，BC=DE，∠B=∠E．求证：∠A=∠F．

    证明见解析 【解析】试题分析：先根据SAS判定△ABD≌△FEC，再根据全等三角形的对应角相等，得出∠A=∠F． 试题解析：证明：∵点B，C，D，E在同一直线上，BC=DE，∴BC+CD=DE+CD，即BD=CE．在△ABD与△FEC中，∵AB=FE，∠B=∠E，BD=CE，∴△ABD≌△FEC（SAS），∴∠A=∠F．

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2016-2017学年八年级上学期期末考试数学试卷 题型：单选题

    如图，BF=EC，∠B=∠E，请问添加下面哪个条件不能判断△ABC≌△DEF（　 ）

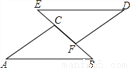
    A. ∠A=∠D B. AB=ED C. DF∥AC D. AC=DF

    D 【解析】试题分析：A、添加∠A=∠D，可用AAS判定△ABC≌△DEF． B、添加AB=ED，可用SAS判定△ABC≌△DEF； C、添加DF∥AC，可证得∠C=∠F，用AAS判定△ABC≌△DEF； D、添加AC=DF，SSA不能判定△ABC≌△DEF． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（华师大版）：期末检测1 题型：填空题

    已知y＋2与x－3成正比例，且当x＝0时，y＝1，则当y＝4时，x的值为________．

    -3 【解析】试题解析：设y+2=k（x-3）， ∵x=0时，y=1， ∴k（0-3）=1+2， 解得：k=-1， ∴y+2=-（x-3）， 即y=-x+1， 当y=4时，则4=-x+1，解得x=-3．

    查看答案和解析>>

    同步练习册答案