
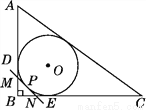
��ͼ��ʾ��Rt��ABC������Բ��O����ֱ�DZ�AB��BC�ֱ������ڵ�D��E�����ӻ�DE(�������˵�D��E)����һ��P����O������MN��AB��BC�ֱ��ڵ�M��N������O�İ뾶Ϊr����Rt��MBN���ܳ�Ϊ________��
 �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д� С����ȫ�ܼ��ϵ�д�
С����ȫ�ܼ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㽭���ݹ�����������ѧ2017-2018ѧ�����꼶��ѧ���п�����ѧ�Ծ����������� ���ͣ������
ˮƽ�������мס��ҡ�������Բ���������������㹻�ߣ�������뾶֮��Ϊ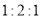 ����������ͬ�Ĺ�����������
����������ͬ�Ĺ�����������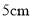 �߶ȴ���ͨ�������ӵ���������
�߶ȴ���ͨ�������ӵ���������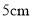 ���������������У�ֻ�м�����ˮ��ˮλ��
���������������У�ֻ�м�����ˮ��ˮλ��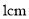 ����ͼ��ʾ����ÿ����ͬʱ���Һͱ�ע����ͬ����ˮ����ʼעˮ
����ͼ��ʾ����ÿ����ͬʱ���Һͱ�ע����ͬ����ˮ����ʼעˮ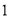 ���ӣ��ҵ�ˮλ����
���ӣ��ҵ�ˮλ����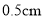 ����ʼע��__________���ӵ�ˮ�������ҵ�ˮλ�߶�֮����
����ʼע��__________���ӵ�ˮ�������ҵ�ˮλ�߶�֮����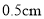 ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017���Ĵ�ʡ�п���ѧģ���Ծ���3�� ���ͣ���ѡ��
���м�����ȷ���ǣ�������
A. 3a+4b=7ab B. ��ab3��2=ab6 C. ��a+2��2=a2+4 D. x12��x6=x6
D �����������������ѡ��A��3a��4b����ͬ������ܺϲ�����ѡ��A����ѡ��B����ab3��3��ab9����ѡ��B����ѡ��C����a��2��2��a2��4a��4, ��ѡ��C����ѡ��x12��x6��x12��6��x6,��ȷ����ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶�˽̰���ѧ�Ծ���C���� ���ͣ������
�Ѷ���ʽ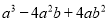 �ֽ���ʽ�Ľ����_______________��
�ֽ���ʽ�Ľ����_______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶�˽̰���ѧ�Ծ���C���� ���ͣ���ѡ��
��ͼ��ijͬѧ��һ�������εIJ�������������飬����Ҫ��������ȥ��һ����ȫһ���IJ�������ô��ʡ�µİ취�ǣ�������
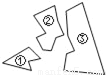
A. ����ȥ B. ����ȥ C. ����ȥ D. ���ٺ͢�ȥ
C �����������������A������ȥ����������ԭ�����ε�һ���ǺͲ��ֱߣ����ܵõ���ԭ��һ���������Σ���Aѡ����� B������ȥ����������ԭ�����ε�һ���ֱߣ�Ҳ�Dz��ܵõ���ԭ��һ���������Σ���Bѡ����� C������ȥ������������ԭ�����ε������ǻ�����������һ���ߣ�����ASA�ж�����Cѡ����ȷ�� D�����ٺ͢�ȥ����������ԭ�����ε�һ���ǺͲ��ֱߣ�ͬ�����ܵõ���ԭ��һ���������Σ���D...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ������
��ͼ��ʾ���ڡ�ABC�У�AB=6��AC=4��P��AC���е㣬��P���ֱ�߽�AB�ڵ�Q������A��P��QΪ����������κ���A��B��CΪ��������������ƣ���AQ�ij�Ϊ_____��
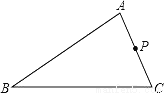
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ���ѡ��
��2015�Ű�����ͼ��ʾ��MN�ǡ�O��ֱ������AB��MN������Ϊ��D������AM��AN����CΪ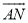 ��һ�㣬��
��һ�㣬��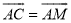 ������CM����AB�ڵ�E����AN�ڵ�F���ָ������½��ۣ���AD=BD���ڡ�MAN=90�㣻��
������CM����AB�ڵ�E����AN�ڵ�F���ָ������½��ۣ���AD=BD���ڡ�MAN=90�㣻��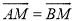 ���ܡ�ACM+��ANM=��MOB����AE=
���ܡ�ACM+��ANM=��MOB����AE=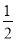 MF��
MF��
������ȷ���۵ĸ����ǣ�������
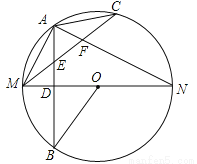
A. 2 B. 3 C. 4 D. 5
D �����������ݴ�����������AB��MN��֪AD=DB, ���ʢ٢���ȷ������ֱ�����Ե�Բ�ܽ�Ϊֱ�ǣ�����MNΪֱ�����õ���MAN=90�㣬�ʢ���ȷ�� ��ͼ�� ����OA���ɣ��õ���MOB=��MOA=2��ACM=��ACM����ANM���ʢ���ȷ�� �ɣ� ���ɵã����Կɵá�AME=��MAE�����ݵȽǶԵȱߣ��õ�AE=ME��Ȼ����ݡ�EAF+��MAE=90�㣬���������á�EFA+��AME...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
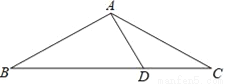
��ͼ���ڡ�ABC�У�AB=AC����C=30�㣬AB��AD��AD=4cm����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ��������棩 ���ͣ���ѡ��
���б����У�����ȷ���ǣ�������
A. a+��b+c��d��=a+b+c��d B. a����b��c+d��=a��b+c��d
C. a��b����c��d��=a��b��c��d D. a+b������c��d��=a+b+c+d
C �����������������A���A����ȷ��B���B����ȷ��C���C���ȷ��D���D����ȷ����ѡC���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com