
以下可以用来证明命题“任何偶数都是4的倍数”是假命题的反例为( )
A. 3 B. 4 C. 8 D. 6
D 【解析】反例就是符合已知条件但不满足结论的例子.可据此找到反例: A、3不是偶数,不符合条件,故错误; B、4是偶数,且能被4整除,故错误; C、8是偶数,且是4的2倍,故错误; D、6是偶数,但是不能被4整除,故正确. 故选:D. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:山东省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
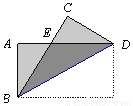
如图,把长方形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:
①△EBD是等腰三角形,EB=ED ;
②折叠后∠ABE和∠CBD一定相等;
③折叠后得到的图形是轴对称图形;
④△EBA和△EDC一定是全等三角形.
其中正确的有( )
A、1个 B、2个 C、3个 D、4个
C. 【解析】 试题分析:根据折叠的性质和平行线的性质可得∠EBD=∠EDB,根据AAS易证△EBA与△EDC全等,①③④是正确,故答案选C.查看答案和解析>>
科目:初中数学 来源:湖南省衡阳市2017-2018学年八年级上期末模拟数学试卷(含答案) 题型:填空题
已知△ABC≌△DEF,且△ABC的三边长分别为3,4,5,则△DEF的周长为 ________ cm.
12 【解析】因为△ABC≌△DEF,所以△ABC和△DEF的周长相等,所以△DEF的周长为:3+4+5=12,故答案为:12.查看答案和解析>>
科目:初中数学 来源:河北省2017-2018学年八年级(上)期末复习测试数学试卷 题型:解答题
计算: 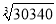 (结果精确到1)
(结果精确到1)
查看答案和解析>>
科目:初中数学 来源:河北省2017-2018学年八年级(上)期末复习测试数学试卷 题型:填空题
如图所示,已知四边形ABCD是等边长为2的正方形,AP=AC,则数轴上点P所表示的数是________.
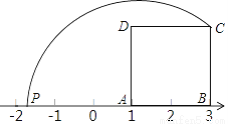
查看答案和解析>>
科目:初中数学 来源:河北省2017-2018学年八年级(上)期末复习测试数学试卷 题型:单选题
用计算器求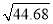 的值为(结果精确到0.01位)( )
的值为(结果精确到0.01位)( )
A. 6.67 B. 6.7 C. 6.70 D. ±6.70
C 【解析】根据计算器的使用方法进行计算即可得≈6.69776≈6.70. 故选:C.查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:解答题
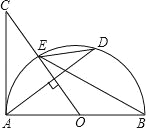
如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,cos∠BED=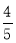 ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:单选题
不等式组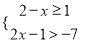 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A. 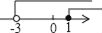 B.
B. 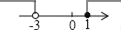 C.
C.  D.
D. 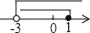
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学模拟试卷(三) 题型:填空题
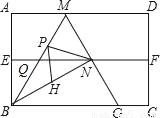
如图,四边形ABCD是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:
①∠ABN=60°;②AM=1;③QN=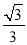 ;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是
;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是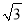 .
.
其中正确结论的序号是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com