
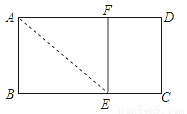
��ͼ����֪����ABCD�У�AB=1����BC��ȡһ��E����AE����ABE�����۵���ʹB������AD�ϵ�F�㣮���ı���EFDC�����ABCD���ƣ���AD=________

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ� ��ʮ���� ��Գ� 13.1 ��Գ� ͬ����ϰ�� ���ͣ������
��ͼ��ʾ,AB-AC=2cm,BC�Ĵ�ֱƽ���߽�AB�ڵ�D,��BC�ڵ�E,��ACD���ܳ���14cm,
��AB��AC�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ѧ�˽̰���꼶�ϲ��11�µڶ������������йصĽǵ�����ʱͬ����ϰ ���ͣ������
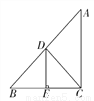
��һ��ֱ�����ǰ���ͼ�ڷţ���C��EF�ϣ�AC������D����֪��A=��EDF=90�㣬AB=AC����E=30�㣬��BCE=40�㣬���CDF=_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��������ɽ�羰��2018����꼶����ĩģ����ѧ�Ծ� ���ͣ������
�������ڽǷֱ������ǶԽǵ�һ����ı��ν�����Խ��ı��Σ�
��1����ͼ1���ڰ�Խ��ı���ABCD�У���B�� ��D����C��
��D����C��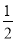 ��A�����B���C�Ķ���֮�ͣ�
��A�����B���C�Ķ���֮�ͣ�
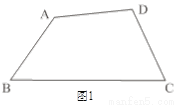
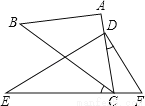
��2����ͼ2����ǡ�ABC�ڽ��ڡ�O������AB�ϴ���һ��D��ʹ��BD��BO����OBA��ƽ���߽�OA�ڵ�E������DE���ӳ���AC�ڵ�F����AFE��2��EAF��
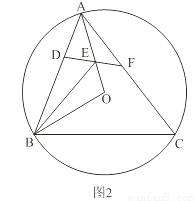
��֤���ı���DBCF�ǰ�Խ��ı��Σ�
��3����ͼ3���ڣ�2���������£�����D��DG��OB�ڵ�H����BC�ڵ�G����DH��BGʱ�����BGH���ABC�����֮�ȣ�
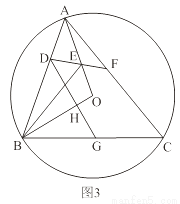
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��������ɽ�羰��2018����꼶����ĩģ����ѧ�Ծ� ���ͣ������
ijũ���⽨������������ң�һ�濿����ǽ��ǽ�㹻�������м���һ��ǽ������������ͼ��ʾ����������1m�����ţ���֪�ƻ��еIJ��Ͽɽ�ǽ�壨�������ţ��ܳ�Ϊ27m�����ܽ��ɵ�������������Ϊ________ m2 ��
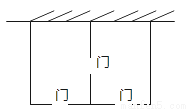
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��������ɽ�羰��2018����꼶����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
��ͼ������ֽƬABCD�У�AB=4��BC=8����ֽƬ�۵���ʹ��C���A�غϣ��ۺ�ΪEF����D�Ķ�Ӧ��ΪG������DG����ͼ����Ӱ��������ǣ� ��
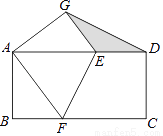
A. 5 B. 3 C. 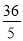 D.
D. 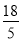
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�����ж�Ǯ����У2018����꼶�ϲ�����������ѧ�Ծ� ���ͣ������
��2016�㽭ʡ�����У��������Σ����ǵ��������Σ�һ����������һ�������ڶԱ��ཻ�������뽻��֮����߶ΰ���������ηָ������С�����Σ�����ֵõ�����С��������һ��Ϊ���������Σ���һ����ԭ���������ƣ����ǰ������߶ν�����������ε������ָ��ߣ�
��1����ͼ1���ڡ�ABC�У�CDΪ��ƽ���ߣ���A=40�㣬��B=60�㣬��֤��CDΪ��ABC�������ָ��ߣ�
��2���ڡ�ABC�У���A=48�㣬CD�ǡ�ABC�������ָ��ߣ��ҡ�ACDΪ���������Σ����ACB�Ķ�����
��3����ͼ2����ABC�У�AC=2��BC=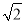 ��CD�ǡ�ABC�������ָ��ߣ��ҡ�ACD����CDΪ�ױߵĵ��������Σ��������ָ���CD�ij���
��CD�ǡ�ABC�������ָ��ߣ��ҡ�ACD����CDΪ�ױߵĵ��������Σ��������ָ���CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�����ж�Ǯ����У2018����꼶�ϲ�����������ѧ�Ծ� ���ͣ���ѡ��
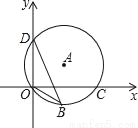
��ͼ����D��0��3����O��0��0����C��4��0���ڡ�A�ϣ�BD�ǡ�A��һ���ң���sin��OBD=��������
A. 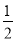 B.
B. 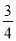 C.
C. 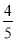 D.
D. 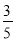
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�갲��ʡ�п���ѧ��ģ�Ծ� ���ͣ���ѡ��
�ס����������һ�������������3�죬Ȼ���Ҽ�����������ʣ�µĹ������蹤������Ϊ1�������������ұ����������������裨������
���� | ��3�� | ��5�� |
�������� |
|
|
A. 9�� B. 10�� C. 11�� D. 12��
A �������������Լ�����x�죬���Լ�����3��=12�죬 ��������ã�2��+��=�� ���x=24 ����£�+��=4�� ����������������4+5=9�� ��ѡA���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com