练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

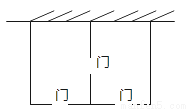
    某农场拟建两间矩形饲养室，一面靠现有墙（墙足够长），中间用一道墙隔开，并在如图所示的三处各留1m宽的门．已知计划中的材料可建墙体（不包括门）总长为27m，则能建成的饲养室面积最大为________ m2 ．

    75 【解析】试题分析：首先设垂直于墙面的长度为x，则根据题意可得：平行于墙面的长度为（30－3x），则S=x（30－3x）=－3+75，,则当x=5时，y有最大值，最大值为75，即饲养室的最大面积为75平方米.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：河南省郑州市郑东新区实验学校2017-2018学年八年级（上）期中数学试卷 题型：单选题

    在平面直角坐标系中，已知线段AB的两个端点分别是A（﹣4，﹣1），B（1，1），将线段AB平移得到线段A′B′，若点A′的坐标为（﹣2，2），则点B′的坐标为（　　）

    A. （3，4） B. （4，3） C. （﹣1，﹣2） D. （﹣2，﹣1）

    A 【解析】由题意可知A（﹣4，﹣1）的对应点A′的坐标为（﹣2，2 ），即可得坐标的变化规律为各对应点之间的关系是横坐标加2，纵坐标加3，由此可得点B′的横坐标为1+2=3，纵坐标为1+3=4，所以点B′的坐标为（3，4）．故选A．

    查看答案和解析>>

    科目：初中数学 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：解答题

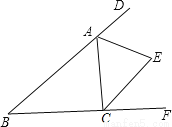
    如图，在△ABC中，∠B=47°，三角形的外角∠DAC和∠ACF的平分线交于点E，求∠AEC的度数．

    66.5° 【解析】试题分析：根据三角形内角和定理、角平分线的定义以及三角形外角定理求得∠DAC+∠ACF=（∠B+∠B+∠1+∠2）=；最后在△AEC中利用三角形内角和定理可以求得∠AEC的度数． 试题解析： ∵三角形的外角∠DAC和∠ACF的平分线交于点E， ∴∠EAC=∠DAC，∠ECA=∠ACF； 又∵∠B=47°（已知），∠B+∠1+∠2=180°（三角形内...

    查看答案和解析>>

    科目：初中数学 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：单选题

    如图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角．关于这七个角的度数关系，下列何者正确（　　）

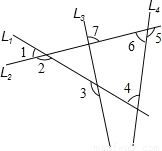
    A. ∠2=∠4+∠7 B. ∠3=∠1+∠6 C. ∠1+∠4+∠6=180° D. ∠2+∠3+∠5=360°

    C 【解析】 A项，根据三角形外角的性质可知，∠2=∠4+∠6，因为L3和L4不平行，所以∠6≠∠7，所以∠2≠∠4+∠7，故A项错误； B项，根据三角形外角的性质可知，∠3=∠AOB+∠OAB，根据对顶角相等可知，∠1=∠AOB，∠7=∠OAB，所以∠3=∠1+∠7，因为L3和L4不平行，所以∠7≠∠6，所以∠3≠∠1+∠6，故B项错误； C项，根据三角形内角和定理可知，...

    查看答案和解析>>

    科目：初中数学 来源：山东省临朐县沂山风景区2018届九年级上期末模拟数学试卷 题型：解答题

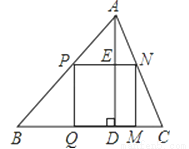
    如图，△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm，要把它加工成正方形零件PQMN，使正方形PQMN的边QM在BC上，其余两个项点P，N分别在AB，AC上．求这个正方形零件PQMN面积S．

    正方形零件PQMN面积是2304mm2. 【解析】试题分析：PN与AD交于点E，如图，设MN=xmm，则AE=AD﹣ED=80﹣x，再证明△APN∽△ABC，利用相似比可表示出PN=（80﹣x），根据正方形的性质得到（80﹣x）=x，然后结合正方形的面积公式进行解答即可． 试题解析：PN与AD交于点E，如图，设MN=xmm， 易得四边形MNED为矩形，则ED=MN=x， ∴...

    查看答案和解析>>

    科目：初中数学 来源：山东省临朐县沂山风景区2018届九年级上期末模拟数学试卷 题型：填空题

    如图，已知矩形ABCD中，AB=1，在BC上取一点E，沿AE将△ABE向上折叠，使B点落在AD上的F点．若四边形EFDC与矩形ABCD相似，则AD=________

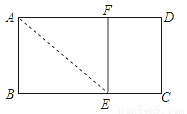
    【解析】试题分析：可设AD=x，由四边形EFDC与矩形ABCD相似，根据相似多边形对应边的比相等列出比例式，求解即可． 【解析】 ∵AB=1， 设AD=x，则FD=x﹣1，FE=1， ∵四边形EFDC与矩形ABCD相似， ∴=，=， 解得x1=，x2=（不合题意舍去）， 经检验x1=是原方程的解． 故答案为．

    查看答案和解析>>

    科目：初中数学 来源：山东省临朐县沂山风景区2018届九年级上期末模拟数学试卷 题型：单选题

    抛物线y=x2－bx+8的顶点在x轴上，取b的值一定为(　　 )

    A. 4 B. -4 C. 2或-2 D. 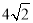或

    D 【解析】∵抛物线y=x2-bx+8的顶点在x轴上， ∴△=（-b)2-4×8=b2-32=0，解得b= ， 故选D．

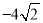
    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型：解答题

    如图，抛物线y1=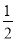（x+1）2+1与y2=a（x﹣4）2﹣3交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于B、C两点，且D、E分别为顶点．则下列结论：①a=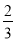；②AC=AE；③△ABD是等腰直角三角形；④当x＞1时，y1＞y2.其中正确结论的个数是（　 　）

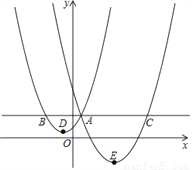
    A. 1个 B. 2个 C. 3个 D. 4个

    B 【解析】【解析】 ∵抛物线与交于点A（1，3），∴3=a（1﹣4）2﹣3，解得：a=，故①正确； ∵E是抛物线的顶点，∴AE=EC，∴无法得出AC=AE，故②错误； 当y=3时，3=，解得：x1=1，x2=﹣3，故B（﹣3，3），D（﹣1，1），则AB=4，AD=BD=，∴AD2+BD2=AB2，∴③△ABD是等腰直角三角形，正确； ∵=时，解得：x1=1，x2=37...

    查看答案和解析>>

    科目：初中数学 来源：2017年安徽省中考数学三模试卷 题型：填空题

    人民公园的侧门口有9级台阶，小聪一步只能上１级台阶或２级台阶，小聪发现当台阶数分别为１级、２级、３级、４级、５级、６级、７级……逐渐增加时，上台阶的不同方法的种数依次为１、２、３、５、８、13、21……这就是著名的斐波那契数列．那么小聪上这９级台阶共有 种不同方法

    55

    查看答案和解析>>

    同步练习册答案