
当1<a<2时,代数式|a﹣2|+|1﹣a|的值是( )
A. ﹣1 B. 1 C. 3 D. ﹣3
B 【解析】知识点是代数式求值及绝对值,根据a的取值范围,先去绝对值符号,再计算求值. 【解析】 当1<a<2时, |a﹣2|+|1﹣a|=2﹣a+a﹣1=1. 故选B. 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源:2018届中考数学专题复习同步练习题:一次函数 题型:解答题
直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的解析式;
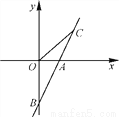
(2)若直线AB上一点C在第一象限且点C的坐标为(2,2),求△BOC的面积.
(1) y=2x-2(2)2 【解析】试题分析:(1)设直线AB的解析式为 将点点分别代入解析式即可组成方程组,从而得到AB的解析式; (2)以OB为底边,C到OB的垂线段为高,根据三角形的面积公式即可求解. 试题解析:(1)设直线AB的解析式为y=kx+b(k≠0), ∵直线AB过点A(1,0)、点B(0,?2), ∴ 解得 ∴直线AB的解析式为y=2x?2; ...查看答案和解析>>
科目:初中数学 来源:人教版初中数学九年级上册第二十一章《配方法解一元二次方程》练习题 题型:填空题
若方程x2-m=0有整数根,则m的值可以是_______________(只填一个)
1(答案不唯一) 【解析】【解析】 若方程x2-m=0有整数根,则x=±,只要m为正整数,且m是完全平方数即可.故m可以取1.故答案为:1(答案不唯一).查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第2章 整式的加减 单元测试卷 题型:填空题
若多项式2x3﹣8x2+x﹣1与多项式3x3+2mx2﹣5x+3相加后不含二次项,则m的值为__.
4. 【解析】∵多项式2?8x²+x?1与多项式3+2mx²?5x+3相加后不含x的二次项, ∴?8x²+2mx²=(2m?8)x², ∴2m?8=0, 解得m=4. 故答案为:4.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第2章 整式的加减 单元测试卷 题型:单选题
下面的计算正确的是( )
A. 6a﹣5a=1 B. a+2a2=3a3 C. ﹣(a﹣b)=﹣a+b D. 2(a+b)=2a+b
C 【解析】试题分析:A.6a﹣5a=a,故此选项错误; B.a与不是同类项,不能合并,故此选项错误; C.﹣(a﹣b)=﹣a+b,故此选项正确; D.2(a+b)=2a+2b,故此选项错误; 故选C.查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:期末达标检测卷 题型:解答题
已知:如图,矩形纸片ABCD的边AD=3,CD=2,点P是边CD上的一个动点(不与点C重合,把这张矩形纸片折叠,使点B落在点P的位置上,折痕交边AD与点M,折痕交边BC于点N .
(1)写出图中的全等三角形. 设CP= 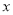 ,AM=
,AM= 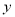 ,写出
,写出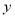 与
与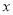 的函数关系式;
的函数关系式;
(2)试判断∠BMP是否可能等于90°. 如果可能,请求出此时CP的长;如果不可能,请说明理由.
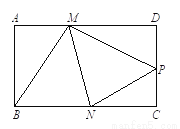
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:期末达标检测卷 题型:填空题
某市为鼓励市民节约用水和加强对节水的管理,制订了以下每月每户用水的收费标准:(1)用水量不超过8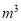 时,每立方米收费1元;(2)超出8
时,每立方米收费1元;(2)超出8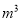 时,在(1)的基础上,超过8
时,在(1)的基础上,超过8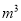 的部分,每立方米收费2元.设某户一个月的用水量为
的部分,每立方米收费2元.设某户一个月的用水量为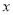
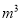 ,应交水费
,应交水费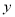 元. 则当
元. 则当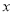 >8时,
>8时, 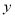 关于
关于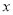 的函数解析式是_______.
的函数解析式是_______.
查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学 第18章 平行四边形 单元检测卷 题型:解答题
(1)如图,纸片?ABCD中,AD=5,S?ABCD=15.过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为( )
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图,在(1)中的四边形纸片AEE/D中,在EE/上取一点F,使EF=4,剪下△AEF,将它平移至△DE/F/的位置,拼成四边形AFF/D.
①求证:四边形AFF'D是菱形;
②求四边形AFF'D的两条对角线的长.
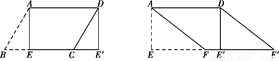
图1 图2
(1)C;(2)①证明见解析;②,3 【解析】试题分析:(1)如图1,纸片?ABCD中,AD=5,S?ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为矩形,故选:C; (2)①证明:∵纸片?ABCD中,AD=5,S?ABCD=15,过点A作AE⊥BC,垂足为E,∴AE=3.如图2: ∵△...查看答案和解析>>
科目:初中数学 来源:福建省莆田市秀屿区2018届九年级上学期期末考试数学试卷 题型:填空题
一个圆锥的底面圆半径为2cm,其侧面展开图的圆心角为120°,则圆锥的母线长是_____________cm.
6 【解析】【解析】 设圆锥的母线长为xcm,根据题意得: =2π•2,解得x=6,即圆锥的母线长为6cm.故答案为:6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com