
求下列各式中的x的值:
(1)(x+10)3=-343;
(2)36(x-3)2=49.
(1)-17 (2)或 【解析】(1)∵(-7)3=-343,∴x+10=-7,∴x=-17. (2)∵36(x-3)2=49,∴, ∵,∴,∴或.科目:初中数学 来源:2017年江苏省徐州市中考数学一模试卷 题型:单选题
如图,是由几个完全相同的小正方体搭建的几何体,它的左视图是( )
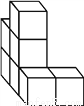
A. 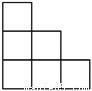 B.
B. 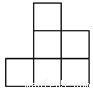 C.
C. 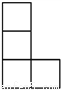 D.
D. 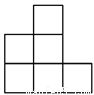
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2017-2018学年八年级上学期教学水平监测数学试卷 题型:填空题
已知,∠ABC=48°,P是∠ABC内一定点,D、E分别是射线BA、BC上的点,当△PDE的周长最小时,∠DPE的度数是__________.
84° 【解析】试题解析:如图作点P关于直线AB的对称点F,作点P关于直线BC的对称点G,连接FG交AB于D,交BC于E,则△PDE的周长最小. 设∠ABP=∠ABF=x,∠CBP=∠CBG=y,则x+y=48°, ∵BP=BF, ∴∠BPF=∠BFP=(180°-2x)=90°-x.同法可得∠BPG=90°-y, ∴∠FPG=180°-x-y=132°, ∴∠...查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2017-2018学年八年级上学期教学水平监测数学试卷 题型:单选题
若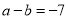 ,
, 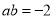 ,则
,则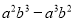 =( )
=( )
A. 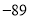 B.
B. 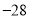 C. 89 D. 28
C. 89 D. 28
查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古呼伦贝尔市七年级(下)期中数学试卷 题型:解答题
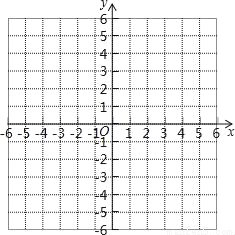
(9分)在平面直角坐标系中,△ABC三个顶点的坐标分别是A(﹣2,2)、B(2,0),C(﹣4,﹣2).
(1)在平面直角坐标系中画出△ABC;
(2)若将(1)中的△ABC平移,使点B的对应点B′坐标为(6,2),画出平移后的△A′B′C′;
(3)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古呼伦贝尔市七年级(下)期中数学试卷 题型:填空题
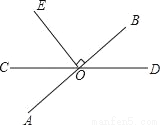
如图,直线AB、CD相交于点O,OE⊥AB于点O,且∠COE=40°,则∠BOD为 .
查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古呼伦贝尔市七年级(下)期中数学试卷 题型:单选题
(2015秋•新泰市期末)在平面直角坐标系中,若点P关于x轴的对称点在第二象限,且到x轴的距离为2,到y轴的距离为3,则点P的坐标为( )
A.(﹣3,﹣2) B.(﹣2,﹣3) C.(2,3) D.(3,2)
A 【解析】 试题分析:根据关于x轴的对称点在第二象限,可得p点在第三象限;根据第三象限内点到x轴的距离是纵坐标,到y轴的距离是横坐标的相反数,可得答案. 【解析】 点P关于x轴的对称点在第二象限,得 O在第三象限, 由到x轴的距离为2,到y轴的距离为3,得 (﹣3,﹣2), 故选:A.查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版八年级数学下册 期中测评 题型:填空题
如图所示,直线y=x+1(记为l1)与直线y=mx+n(记为l2)相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为__________.
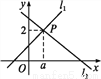
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2018届九年级上学期教学水平监测数学试卷 题型:单选题
如图,在△ABC中,M,N分别是边AB,AC的中点,则△AMN的面积与四边形MBCN的面积比为
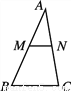
A.  B.
B.  C.
C.  D.
D. 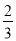
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com