练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    抛物线图象如图所示，根据图象，抛物线的解析式可能是（　　）

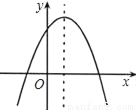
    A. y=x2﹣2x+3 B. y=﹣x2﹣2x+3 C. y=﹣x2+2x+3 D. y=﹣x2+2x﹣3

    C 【解析】试题解析：由图象得：a<0，b>0，c>0. 故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：青海省2017-2018学年七年级上学期12月月考数学试卷 题型：单选题

    比-3小1的数是 （ ）

    A. 2 B. -2 C. 4 D. -4

    D 【解析】试题解析：-3-1=-4． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型：填空题

    如图，下面两个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色，那么黄色的对面是_________．

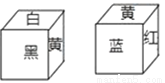
    绿色 【解析】试题分析：分析可知黄色的对面是绿色，白色的对面是蓝色，红色的对面是黑色.

    查看答案和解析>>

    科目：初中数学 来源：2017年贵州省中考数学二模试卷 题型：解答题

    如图，已知⊙O的直径AB与弦CD互相垂直，垂足为点E. ⊙O的切线BF与弦AD的延长线相交于点F，且AD=3，cos∠BCD= .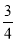

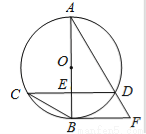
    （1）求证：CD∥BF；

    （2）求⊙O的半径；

    （3）求弦CD的长.

    （1）见解析（2）2（3） 【解析】【解析】 （1）∵BF是⊙O的切线 ∴AB⊥BF …………………1分 ∵AB⊥CD ∴CD∥BF………………………………………………2分 （2）连结BD ∵AB是直径 ∴∠ADB=90° ………………………………………3分 ∵∠BCD=∠BAD cos∠BCD=…………………4分 ∴cos∠BAD= 又∵AD=3...

    查看答案和解析>>

    科目：初中数学 来源：2017年贵州省中考数学二模试卷 题型：填空题

    观察下列等式：

    在上述数字宝塔中，从上往下数，2016在第_____层.

    44 【解析】试题分析：首先得出每一层的第一个数字为，每一行数的个数为2n+1个，然后根据规律得出答案.

    查看答案和解析>>

    科目：初中数学 来源：2017年贵州省中考数学二模试卷 题型：单选题

    如图，直线AB∥CD，∠1=50°，∠2=110°，则∠E的大小是（ ）.

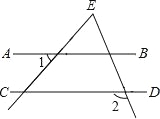
    A．40° B．50° C．60° D．30°

    C． 【解析】 试题分析：先根据平行线的性质求出∠3的度数，再根据三角形的外角性质求出即可．如图：∵AB∥CD，∠1=50°，∴∠3=∠1=50°，∵∠2=110°，∴∠E=∠2﹣∠3=110°﹣50°=60°，故选C．

    查看答案和解析>>

    科目：初中数学 来源：黄金30题系列 九年级数学 大题易丢分 题型：解答题

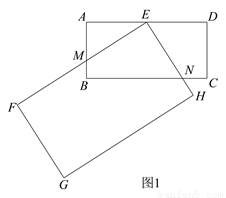
    问题背景

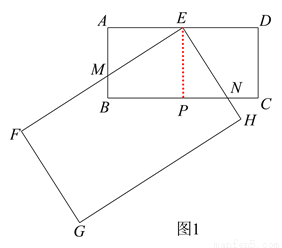
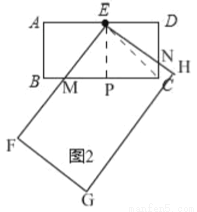
    在数学活动课上，张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动．如图 1，在矩形纸片ABCD 和矩形纸片EFGH中，AB＝1，AD＝2，且FE＞AD，FG＞AB，点E 是 AD 的中点，矩形纸片 EFGH 以点E 为旋转中心进行逆时针旋转，在旋转过程中会产生怎样的数量关系，提出恰当的数学问题并加以解决．

    解决问题

    下面是三个学习小组提出的数学问题，请你解决这些问题．

    （1）“奋进”小组提出的问题是：如图 1，当 EF 与 AB 相交于点 M，EH 与 BC 相交于点 N 时，求证：EM=EN．

    （2）“雄鹰”小组提出的问题是：在（1）的条件下，当 AM=CN 时，AM 与 BM 有怎样的数量关系，请说明理由．

    （3）“创新”小组提出的问题是：若矩形 EFGH 继续以点 E 为旋转中心进行逆时针旋转，当 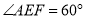时，请你在图 2 中画出旋转后的示意图，并求出此时 EF 将边 BC 分成的两条线段的长度．

    【答案】（1）证明见解析；（2）AM=BN；（3）EF 将边 BC 分成的两条线段的长度为 ．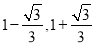

    【解析】试题分析：（1）过点 E 作 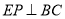，垂足为点P，根据已知条件证出PE=AE，再证得∠PEN=∠AEM，进而得到△PEN≌△AEM，即可证得结论；（2）易证PN=CN= 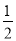PC，进而求出PN=CN=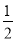，再判断出AM=PN=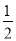，即可得出BM=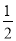，从而证得结论；（3）在Rt△PEM中，求出PM的长，再用线段的和差即可得出结论．

    试题解析：

    （1） 如图1，过点 E 作 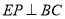，垂足为点 P，

    则四边形 ABPE 是矩形，∴PE=AB=1， ，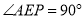

    ∵ 点 E 是 AD 的中点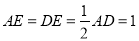，∴ ，∴PE=AE，

    ∵ ，∴ ，

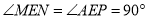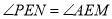    ∵PE=AE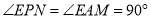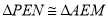， ，∴，∴EM=EN．

    （2） 由（1）知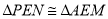， ，∴AM=PN，

    ∵AM=CN，∴PN=CN=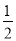PC，

    ∵ 四边形 EPCD 是矩形，∴PC=DE=1，PN=CN=，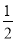

    ∴AM=PN=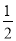，BM=AB-AM=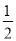，∴AM=BN．

    （3）如图2，当∠AEF=60°时，

    设EF与BC交于M，EH与CD交于N，过点E作EP⊥BC于P，连接EC，

    由（1）知，CP=EP=1，AD∥BC，

    ∴∠EMP=∠AEF=60°，

    在Rt△PEM中，PM=，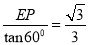

    ∴BM=BP﹣PM=1﹣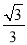，CM=PC+PM=1+，

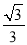    ∴EF将边BC分成的两条线段的长度为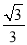1﹣，1+．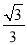

    【题型】解答题
    【结束】
    20

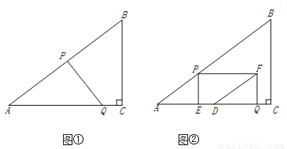
    如图①，在Rt△ABC中，∠C=90°，AB=10，BC=6．点P从点A出发，沿折现AB—BC向终点C运动，在AB上以每秒5个单位长度的速度运动，在BC上以每秒3个单位长度的速度运动．点Q从点C出发，沿CA方向以每秒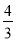个单位长度的速度运动．点P、Q两点同时出发，当点P停止时，点Q也随之停止．设点P运动的时间为t秒．

    （1）求线段AQ的长．（用含t的代数式表示）

    （2）当PQ与△ABC的一边平行时，求t的值

    （3）如图②，过点P作PE⊥AC于点E，以PE、QE为邻边作矩形PEQF，点D为AC的中点，连结DF．直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值．

    （1）AQ=8-t（0≤t≤4）； （2）t=s或3s时，当PQ与△ABC的一边平行； （3）①S=；②当t=s或s时，DF将矩形PEQF分成两部分的面积比为1：2. 【解析】试题分析：（1）利用勾股定理先求出AC，根据AQ=AC-CQ即可解决问题； （2）分两种情形列出方程求解即可； （3）①分三种情形a、如图1中，当0≤t≤时，重叠部分是四边形PEQF．b、如图2...

    查看答案和解析>>

    科目：初中数学 来源：黄金30题系列 九年级数学 大题易丢分 题型：解答题

    “校园安全”受到全社会的广泛关注，某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了两幅尚不完整的统计图，如图所示，请根据统计图中所提供的信息解答下列问题：

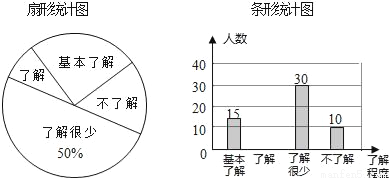
    （1）接受问卷调查的学生共有　 　人，扇形统计图中“基本了解”部分所对应扇形的圆心角为　 　；

    （2）请补全条形统计图；

    （3）若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率．

    （1）60；90°；（2）补图见解析；（3） 【解析】试题分析：（1）根据了解很少的人数和所占的百分百求出抽查的总人数，再用“基本了解”所占的百分比乘以360°，即可求出“基本了解”部分所对应扇形的圆心角 的度数； （2）用调查的总人数减去“基本了解”“了解很少”和“基本了解”的人数，求出了解的人数，从而补全统计图； （3）根据题意先画出树状图，再根据概率公式即可得出答案．...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷（A卷） 题型：填空题

    如图，△ABC中，∠ACB=90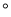，BC=3cm，CD⊥AB于D，在AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F，若EF=5cm，则AE=______cm.

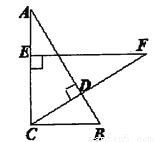
    2 【解析】试题解析：∵EF⊥AC， ∴∠FEC=90°， ∵CD⊥AB， ∴∠ADF=90°， ∴∠A=∠F， 在△ACB和△FEC中 ， ∴△ACB≌△FEC（AAS）， ∴AC=EF=5cm， 而EC=BC=3cm， ∴AE=5cm-3cm=2cm．

    查看答案和解析>>

    同步练习册答案