练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    观察下列等式：

    在上述数字宝塔中，从上往下数，2016在第_____层.

    44 【解析】试题分析：首先得出每一层的第一个数字为，每一行数的个数为2n+1个，然后根据规律得出答案.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：青海省2017-2018学年七年级上学期12月月考数学试卷 题型：单选题

    如图，点A、O、B在同一直线上，CO⊥AB于点O，若∠1＝∠2，则图中互余的角共有(　　)

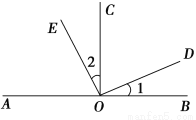
    A．5对 B．4对

    C．3对 D．2对

    B 【解析】∵CO⊥AB，∴ ∠AOC＝∠BOC＝90°， ∴∠1＋∠COD＝90°，∠2＋∠AOE＝90°. 又∵∠1＝∠2，∴∠2＋∠COD＝90°， ∠2＋∠AOE＝90°.即图中互余的角有4对．

    查看答案和解析>>

    科目：初中数学 来源：江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型：解答题

    先化简，再求值已知A=x2-2x-1, B=2x2-6x+3, 求3A-[(2A-B)-2(A-B)]的值,其中x=-7.

    43 【解析】试题分析：首先根据去括号的法则将括号去掉进行化简在去括号时，如果括号前面是负号，则去掉括号后要注意变号；然后将A和B的值代入再进行化简，最后将x的值代入化简后的式子进行计算得出答案． 试题解析：【解析】 3A-[（2A-B）-2（A-B）] =3A-2A+B+2A-2B =3A-B． 当A=x2-2x-1，B=2x2-6x+3时，原式=x2-6． 当x=-7时，...

    查看答案和解析>>

    科目：初中数学 来源：江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型：单选题

    下列各式：①﹣（﹣2）；②﹣|﹣2|；③﹣22；④﹣（﹣2）2，计算结果为负数的个数有（ ）.

    A. 4个 B. 3个 C. 2个 D. 1个

    B 【解析】∵①－(－2)=2>0；②－|－2|=-2<0；③－22=-4<0；④－(－2)2=-4<0; ∴计算结果为负数的个数有3个。 故选B.

    查看答案和解析>>

    科目：初中数学 来源：2017年贵州省中考数学二模试卷 题型：解答题

    我省某地区为了了解2016年初中毕业生毕业去向，对部分九年级学生进行了抽样调查，就九年级学生毕业后的四种去向：A．读普通高中；B．读职业高中；C．直接进入社会就业；D．其他（如出国等）进行数据统计，并绘制了两幅不完整的统计图（如图1，如图2）

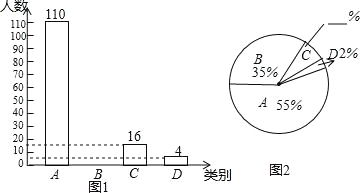
    （1）填空：该地区共调查了 名九年级学生；

    （2）将两幅统计图中不完整的部分补充完整；

    （3）若该地区2016年初中毕业生共有3500人，请估计该地区今年初中毕业生中读普通高中的学生人数；

    （4）老师想从甲，乙，丙，丁4位同学中随机选择两位同学了解他们毕业后的去向情况，请用画树状图或列表的方法求选中甲同学的概率．

    (1)200;(2)详见解析；（3）1925；（4）. 【解析】 试题分析：（1）根据统计图可以得到本次调查的九年级学生数；（2）根据题目中的数据可以得到统计图中未知的数据，从而可以解答本题；（3）根据统计图中的数据可以估计该地区今年初中毕业生中读普通高中的学生人数；（4）根据题意可以画出相应的树状图，从而可以求得选中甲同学的概率． 试题解析：（1）该地区调查的九年级学生数为：1...

    查看答案和解析>>

    科目：初中数学 来源：2017年贵州省中考数学二模试卷 题型：单选题

    抛物线图象如图所示，根据图象，抛物线的解析式可能是（　　）

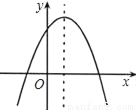
    A. y=x2﹣2x+3 B. y=﹣x2﹣2x+3 C. y=﹣x2+2x+3 D. y=﹣x2+2x﹣3

    C 【解析】试题解析：由图象得：a<0，b>0，c>0. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017年贵州省中考数学二模试卷 题型：单选题

    如图，在△ABC中，点D、E分AB、AC边上，DE∥BC，若AD：AB=3：4，AE=6，则AC等于（　　）

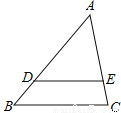
    A．3 B．4 C．6 D．8

    D 【解析】 首先由DE∥BC可以得到AD：AB=AE：AC，而AD：AB=3：4，AE=6，由此即可求出AC． 【解析】 ∵DE∥BC， ∴△ADE∽△ABC， ∴AD：AB=AE：AC， 而AD：AB=3：4，AE=6， ∴3：4=6：AC， ∴AC=8． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：黄金30题系列 九年级数学 大题易丢分 题型：解答题

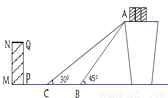
    如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°. 已知原传送带AB长为4米.

    （1）求新传送带AC的长度；

    （2）如果需要在货物着地点C的左侧留出2米的通道，试判断距离B点4米的货物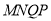是否需要挪走，并说明理由．

    【答案】（1）5.6m；（2）应挪走．

    【解析】试题解析：试题分析：（1）在构建的直角三角形中，首先求出两个直角三角形的公共直角边，进而在Rt△ACD中，求出AC的长．
    （2）通过解直角三角形，可求出BD、CD的长，进而可求出BC、PC的长．然后判断PC的值是否大于2米即可．

    试题解析：（1）如图，
    在Rt△ABD中，AD=ABsin45°=4．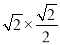 
    在Rt△ACD中，
    ∵∠ACD=30°，
    ∴AC=2AD=8． 
    即新传送带AC的长度约为8米；
    （2）结论：货物MNQP不用挪走． 
    【解析】
    在Rt△ABD中，BD=ABcos45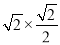°=4=4． 
    在Rt△ACD中，CD=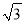AD=4．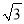
    ∴CB=CD-BD=4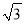-4≈2.8．
    ∵PC=PB-CB≈5-2.8=2.2＞2，
    ∴货物MNQP不应挪走．

    【题型】解答题
    【结束】
    8

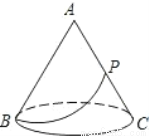
    如图有一圆锥形粮堆，其主视图是边长为6m的正三形ABC。

    （1）求该圆锥形粮堆的侧面积。

    （2）母线AC的中点P处有一老鼠正在偷吃粮食，小猫从B处沿圆锥表面去偷袭老鼠，求小猫经过的最短路程。 (结果不取近似数) 

    （1) 18m2；（2）3m. 【解析】试题分析：（1）根据圆锥的侧面展开图是扇形，圆锥的侧面积公式是π×底面圆半径×圆锥的母线长；扇形的面积公式是，进行计算即可； （2）根据两点之间，线段最短．首先要展开圆锥的半个侧面，再连接BP．发现BP是直角边是3和6的直角三角形的斜边．根据勾股定理即可计算． 试题解析：（1）根据圆锥的侧面积等于展开扇形的面积得： πrl=π×3×6=18π...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷（A卷） 题型：解答题

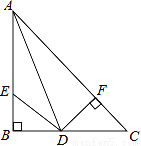
    如图，△ABC中，AD为∠BAC的平分线，且DF⊥AC于F，∠B=90°，DE=DC．求证：BE=CF．

    证明见解析. 【解析】试题分析：利用角平分线构造的全等三角形，再用HL证明Rt△BDE和Rt△FDC全等. 试题解析： 证明：∵∠B=90°， ∴BD⊥AB， ∵AD为∠BAC的平分线，且DF⊥AC， ∴DB=DF， 在Rt△BDE和Rt△FDC中， ， ∴Rt△BDE≌Rt△FDC（HL）， ∴BE=CF．

    查看答案和解析>>

    同步练习册答案