
��У��ȫ���ܵ�ȫ���Ĺ㷺��ע��ij��ѧ�Բ���ѧ����У��ȫ֪ʶ���˽�̶ȣ����������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ������������в�������ͳ��ͼ����ͼ��ʾ�������ͳ��ͼ�����ṩ����Ϣ����������⣺
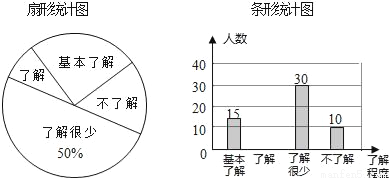
��1�������ʾ������ѧ�������� ���ˣ�����ͳ��ͼ�С������˽⡱��������Ӧ���ε�Բ�Ľ�Ϊ�� ����
��2���벹ȫ����ͳ��ͼ��
��3�����Ӷ�У��ȫ֪ʶ�ﵽ�ˡ��˽⡱�̶ȵ�3��Ů����2�������������ȡ2�˲μ�У��ȫ֪ʶ������������״ͼ���б������ǡ�ó鵽1��������1��Ů���ĸ��ʣ�
��1��60��90�㣻��2����ͼ����������3�� �������������������1�������˽���ٵ���������ռ�İٷְ�������������������á������˽⡱��ռ�İٷֱȳ���360�㣬��������������˽⡱��������Ӧ���ε�Բ�Ľ� �Ķ����� ��2���õ������������ȥ�������˽⡱���˽���١��͡������˽⡱������������˽���������Ӷ���ȫͳ��ͼ�� ��3�����������Ȼ�����״ͼ���ٸ��ݸ��ʹ�ʽ���ɵó��𰸣�... �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ��̨�е�����������2017-2018ѧ��ȵ�һѧ�ڵ����νμ�����꼶��ѧ�Ծ� ���ͣ������
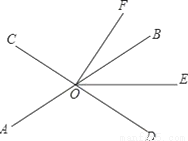
��ͼ��ֱ��AB��CD�ཻ�ڵ�O��OEƽ�֡�BOD��
��1������AOC=70�㣬��DOF=90�㣬���EOF�Ķ�����
��2����OFƽ�֡�COE����BOF=15�㣬�����AOE=x�㣮
���ú�x�Ĵ���ʽ��ʾ��EOF;
�����AOC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧ��ģ�Ծ� ���ͣ���ѡ��
������ͼ����ͼ��ʾ������ͼ�������ߵĽ���ʽ�����ǣ�������
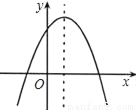
A. y=x2��2x+3 B. y=��x2��2x+3 C. y=��x2+2x+3 D. y=��x2+2x��3
C �������������������ͼ��ã�a<0��b>0��c>0. ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ �������� ���ͣ������
��ͼ����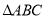 �У�
�� 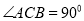 ����
����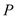 ��
��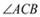 ���ߵľ�����ȣ���
���ߵľ�����ȣ��� ��
��
��1�����ó߹���������Ҫ��ĵ�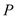 ��������ͼ�ۼ�������Ҫд��������Ȼ���жϡ�ABP����״����˵�����ɣ�
��������ͼ�ۼ�������Ҫд��������Ȼ���жϡ�ABP����״����˵�����ɣ�
��2����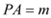 ��
��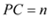 ������
������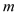 ��
��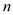 �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ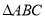 ���ܳ��������
���ܳ��������
��3���� ��
��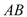 ���ڵ�
���ڵ�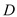 ����̽������
����̽������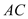 ��
��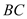 �ij��ȱ仯ʱ��
�ij��ȱ仯ʱ��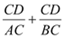 ��ֵ�Ƿ����仯�������䣬�������������ֵ�����仯����˵�����ɣ�
��ֵ�Ƿ����仯�������䣬�������������ֵ�����仯����˵�����ɣ�
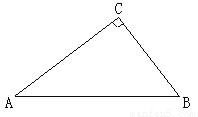
���𰸡�(1)��ͼ����������ABP�ǵ���ֱ��������. ���ɼ���������2��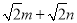 ��
�� 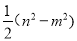 ��3��
��3��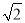 .
.
��������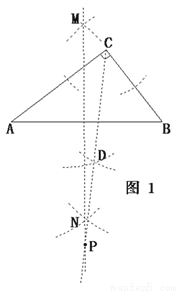 ��1�������⣬��P����
��1�������⣬��P����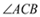 ��ƽ�����ϣ�
��ƽ�����ϣ�
�����߶�AB�Ĵ�ֱƽ������.
��ͼ1����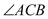 ��ƽ����
��ƽ����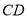 ��
��
���߶�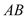 �Ĵ�ֱƽ����
�Ĵ�ֱƽ����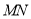 ��
�� 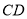 ��
��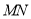 ��
��
���㼴Ϊ�����P�㡣��������������������������������3��
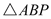 �ǵ���ֱ��������.
�ǵ���ֱ��������.
���ɣ�����P�ֱ��� ��
�� ������ΪE��F��ͼ2.
������ΪE��F��ͼ2.
�� ƽ��
ƽ��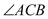 ��
�� ��
�� ������ΪE��F��
������ΪE��F��
�� .
.
�֡�  ����
����  ��
��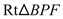 .����������������4��
.����������������4��
��  .
.
��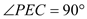 ��
��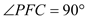 ��
�� ��
��
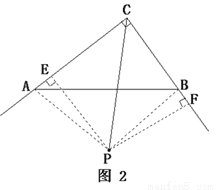 ��
��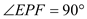 �� �Ӷ�
�� �Ӷ�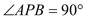 .
.
�� ��
�� 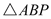 �ǵ���ֱ��������. ����������������5��
�ǵ���ֱ��������. ����������������5��
��2����ͼ2���� �У�
��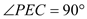 ��
��
 ��
��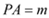 . ��
. �� .
.
�� ��
��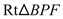 ��
��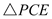 ��
��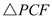 ��
��
�ɵ� ��
�� .
.
��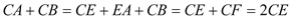 .
.
�� ��
��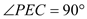 ��
��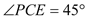 ��
�� ��
��
��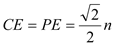 . ��
. �� . ��������6��
. ��������6��
����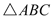 ���ܳ�Ϊ��
���ܳ�Ϊ�� . ��������7��
. ��������7��
��Ϊ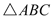 �����=
�����=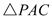 �����
�����
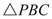 �����
�����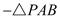 �����
�����
=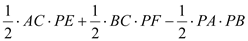 =
=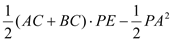
=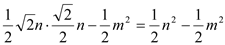 ��
��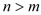 ������9��
������9��
�� 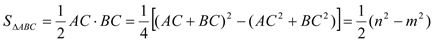 .
.
��3������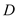 �ֱ���
�ֱ���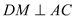 ��
�� ������Ϊ
������Ϊ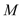 ��
�� ��ͼ3.
��ͼ3.
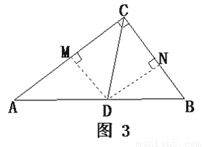 ��
�� 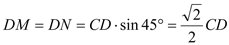 .��������10��
.��������10��
�� ��
��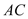 ��
�� 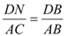 �٩���������������11��
�٩���������������11��
�� ��
��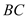 ��
�� 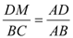 �� ������������12��
�� ������������12��
��+�ڣ��� 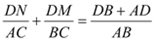 ����
���� 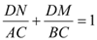 .
.
�� 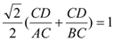 �� ��
�� �� 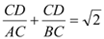 ��������13��
��������13��
���㾦����1��������������ACB�Ľ�ƽ���ߺ��߶�AB�Ĵ�ֱƽ���߿������P��Ȼ��֤��Rt��APE��Rt��BPF���ɣ�
��2����PA=PB��PA=m���ɵó�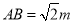 ����Rt��APE��Rt��BPF����PCE�ա�PCF���ɵ�CA+CB=CE+EA+CB=CE+CF=2CE����Rt��PCE�У� PC=n����֪
����Rt��APE��Rt��BPF����PCE�ա�PCF���ɵ�CA+CB=CE+EA+CB=CE+CF=2CE����Rt��PCE�У� PC=n����֪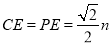 ����
����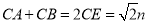 ���������ܳ��������
���������ܳ��������
��3����ƽ���߷��߶γɱ��������õ�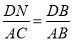 ,
, 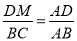 �ǽ����Ĺؼ���
�ǽ����Ĺؼ���
�����͡������
��������
15
��O�ǡ�ABC�����Բ��AB��ֱ������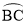 ���е�P����O��ֱ��PG������BC�ཻ�ڵ�D������AG��CP��PB��
���е�P����O��ֱ��PG������BC�ཻ�ڵ�D������AG��CP��PB��
��1����ͼ1����֤��AG=CP��
��2����ͼ2������P��AB�Ĵ��ߣ�����Ϊ��H������DH����֤��DH��AG��
��3����ͼ3������PA���ӳ�HD�ֱ���PA��PC�ཻ�ڵ�K��F����֪FK=2����ODH�����Ϊ2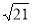 ����AC�ij���
����AC�ij���
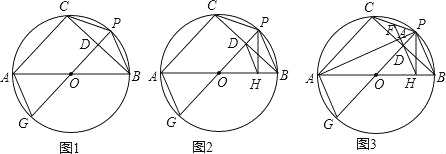
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ �������� ���ͣ������
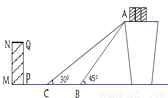
��ͼ��ij��վ���ͻ����ƽ��ʾ��ͼ. Ϊ����ߴ����̵İ�ȫ�ԣ�����ʦ������С���ʹ������ļнǣ�ʹ����45���Ϊ30��. ��֪ԭ���ʹ�AB��Ϊ4��.
��1�����´��ʹ�AC�ij��ȣ�
��2�������Ҫ�ڻ����ŵص�C���������2��ͨ�������жϾ���B��4�Ļ���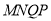 �Ƿ���ҪŲ�ߣ���˵�����ɣ�
�Ƿ���ҪŲ�ߣ���˵�����ɣ�
���𰸡���1��5.6m����2��ӦŲ�ߣ�
����������������������������1���ڹ�����ֱ���������У������������ֱ�������εĹ���ֱ�DZߣ�������Rt��ACD�У����AC�ij���
��2��ͨ����ֱ�������Σ������BD��CD�ij������������BC��PC�ij���Ȼ���ж�PC��ֵ�Ƿ����2���ɣ�
�����������1����ͼ��
��Rt��ABD��AD=ABsin45��=4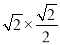 ��
��
��Rt��ACD��
�ߡ�ACD=30�㣬
��AC=2AD=8��
���´��ʹ�AC�ij���ԼΪ8�ף�
��2�����ۣ�����MNQP����Ų�ߣ�
��������
��Rt��ABD��BD=ABcos45��=4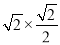 =4��
=4��
��Rt��ACD��CD=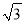 AD=4
AD=4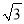 ��
��
��CB=CD-BD=4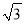 -4��2.8��
-4��2.8��
��PC=PB-CB��5-2.8=2.2��2��
�����MNQP��ӦŲ�ߣ�
�����͡������
��������
8
��ͼ��һԲ�����ѣ�������ͼ�DZ߳�Ϊ6m��������ABC��
��1�����Բ�����ѵIJ������
��2��ĸ��AC���е�P����һ��������͵����ʳ��Сè��B����Բ����ȥ͵Ϯ������Сè���������·�̡� (�����ȡ������)
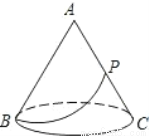
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ������
һ���̵��ij����Ʒ���������20%��Ϊ���ۣ�������������ȥ�����������ۼ���20%���ۣ��ܿ��������������������4Ԫ����ô�����Ʒ�Ľ�����________Ԫ��
100 ����������������ɵù���x�ķ��̣����ɵ���Ʒ�Ľ��ۣ� �������� �������⣺��δ֪����Ϊx�� �ɵã�x•��1+20%��•��1-20%��=96 ��ã�x=100���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ������
�Ϧ��IJ��DZȡϦ�����ǵ�3����10�㣬��Ϧ�=__________��
50�� ��������������ǺͲ��ǵĸ����г����̣��ⷽ�̼��ɣ� �������� ��Ϧ�=x�� ������ã�180�㩁x=3��90�㩁x��+10�㣬 ��ã�x=50�㣬 �ʴ�Ϊ��50�㣮 ���㾦�����⿼�������ǺͲ��ǵĸ�������������ǵĺ�Ϊ90�㣬���������ǻ��ࣻ�������ǵĺ͵���180�㣬���������ǻ����ǽ���Ĺؼ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ���ѡ��
��ͼ������˵������ȷ���ǣ�������
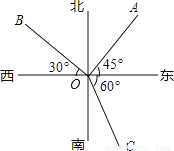
A. OC�ķ�������ƫ��30�� B. OA�ķ����DZ�ƫ��45��
C. OB�ķ�������ƫ��30�� D. ��AOB�Ķ�����75��
D ���������⣺A�� OC�ķ�������ƫ��30�� ����ȷ�� B�� OA�ķ����DZ�ƫ��45�㣬��ȷ�� C�� OB�ķ�������ƫ��30�� ����ȷ�� D�� ��AOB�Ķ�����180��-75��=105�㣬���� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶��ʦ�����ѧ�Ծ���B���� ���ͣ������
��ֱ��nx+��n+1��y=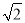 ��nΪ��Ȼ��������������Χ�ɵ����������ΪSn����S1+S2+��+S2016��ֵΪ__��
��nΪ��Ȼ��������������Χ�ɵ����������ΪSn����S1+S2+��+S2016��ֵΪ__��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com