解方程:3x(x-1)=2x-2. x1=.x2=1 [解析]方程变形得:3x. 移项.因式分解得=0. 解得x1=.x2=1. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

解方程：3x(x－1)=2x－2.(因式分解法)

x1=，x2=1 【解析】方程变形得：3x(x－1)=2(x－1)，移项，因式分解得(3x－2)(x－1)=0，解得x1=，x2=1.

练习册系列答案

初中学业水平考试历史与社会思想品德精讲精练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：江苏省2018届九年级12月月考数学试卷 题型：单选题

二次函数y=ax2+bx+c（≠0）的图象如图，给出下列四个结论：①4ac﹣b2＜0；②3b+2c＜0；③4a+c＜2b；④m（am+b）+b＜a（m≠1），其中结论正确的个数是（）

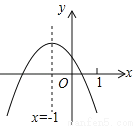
A．1 B．2 C．3 D．4

B．【解析】试题解析：∵图象与x轴有两个交点， ∴方程ax2+bx+c=0有两个不相等的实数根， ∴b2﹣4ac＞0， ∴4ac﹣b2＜0， ①正确； ∵﹣=﹣1， ∴b=2a， ∵a+b+c＜0， ∴b+b+c＜0，3b+2c＜0， ∴②是正确； ∵当x=﹣2时，y＞0， ∴4a﹣2b+c＞0， ∴4a+c＞...

查看答案和解析>>

科目：初中数学 来源：人教版九年级数学上册经典试卷第21章一元二次方程韦达定理测试卷 题型：解答题

已知关于x的方程x2+2mx-(m+1)=0，若两根倒数的和比两根倒数的积小1，求m的值.

【解析】试题分析：根据一元二次方程的根与系数的关系列式求解即可. 试题解析：设方程的两根为，x2，则x1+x2=-2m，x1x2=-(m+1)，由题意可知：，即： ∴，解得： . 此时：方程有实根 ∴

查看答案和解析>>

科目：初中数学 来源：人教版九年级数学上册经典试卷第21章一元二次方程韦达定理测试卷 题型：单选题

关于x的一元二次方程x2+2(m-1)x+m2=0的两个实数根分别为x1,x2且x1+x2>0,x1x2>0，则m的取值范围是( )

A. m≤ B. m≤且m≠0 C. m<1 D. m<1且m≠0

B 【解析】由题意得，，解之得，m<1且m≠0. 又∵△=4(m-1)2-4m2≥0，解之得， . ∴m的取值范围是且m≠0.故选B.