
科目:初中数学 来源:湖南省衡阳市2018届九年级上期末模拟数学试卷 题型:解答题
曲靖市某楼盘准备以每平方米4000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米3240元的均价开盘销售.
(1)求平均每次下调的百分率;
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.9折销售;②不打折,送两年物业管理费,物业管理费是每平方米每月1.4元,请问哪种方案更优惠?
(1)平均每次下调的百分率是10%; (2)选择方案②更优惠,理由见解析. 【解析】试题分析: (1)设平均每次下调的百分率为,根据题意列出一元二次方程,解方程即可得到符合要求的答案; (2)根据题意分别计算出两种方案的优惠金额,在比较大小即可得到答案; 试题解析: (1)设平均每次下调的百分率是x,依题意得: 4000(1﹣x)2=3240 ,解得:x=...查看答案和解析>>
科目:初中数学 来源:浙江杭州上城区北师大附属杭州中学2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
已知二次函数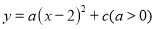 ,当自变量
,当自变量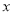 分别取
分别取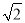 、
、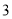 、
、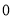 时,对应的函数值分别:
时,对应的函数值分别: 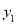 ,
, 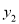 ,
, 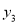 ,则
,则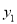 ,
, 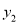 ,
, 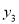 的大小关系正确的是( ).
的大小关系正确的是( ).
A. 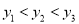 B.
B. 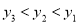 C.
C. 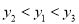 D.
D. 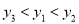
查看答案和解析>>
科目:初中数学 来源:重庆市2017年中考数学二模试卷 题型:填空题
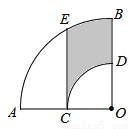
如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC为半径作弧CD交OB于点D,若OA=2,则阴影部分的面积为______.
查看答案和解析>>
科目:初中数学 来源:重庆市2017年中考数学二模试卷 题型:单选题
已知△ABC∽△DEF,S△ABC:S△DEF=1:9,若BC=1,则EF的长为( )
A. 1 B. 2 C. 3 D. 9
C 【解析】【解析】 ∵△ABC∽△DEF,S△ABC:S△DEF=1:9,∴BC:EF=1:3,∵BC=1,∴EF的长为:3.故选C.查看答案和解析>>
科目:初中数学 来源:广东省河源市和平县2017-2018学年七年级(上)期中数学试卷(解析版) 题型:解答题
司机小王沿东西大街跑出租车,约定向东为正,向西为负,某天自A地出发到收工时,行走记录为(单位:千米):+8、﹣9、+7、﹣2、+5、﹣10、+7、﹣3,回答下列问题:
(1)记录中“+8”表示什么意思?
(2)收工时小王在A地的哪边?距A地多少千米?
(3)若每千米耗油0.2升,问从A地出发到收工时,共耗油多少升?
(1)小王向东走了8千米; (2)收工时小王在A地的东边,距A地3千米; (3)从A地出发到收工时,共耗油10.2升. 【解析】试题分析:(1)向东为正,“+8”表示向东走了8千米; (2)根据有理数的加法,可得答案; (3)根据单位耗油量乘以行驶路程,可得耗油量; 试题解析:(1)记录中“+8”表示小王向东走了8千米; (2)8+(﹣9)+7+(﹣2)+5+...查看答案和解析>>
科目:初中数学 来源:广东省河源市和平县2017-2018学年七年级(上)期中数学试卷(解析版) 题型:填空题
世界文化遗产长城总长约为6700000m,将6700000用科学记数法表示应为_____.
6.7×106 【解析】试题解析:6700000用科学记数法表示为: 故答案为:查看答案和解析>>
科目:初中数学 来源:2017年重庆市中考数学模拟试卷 题型:解答题
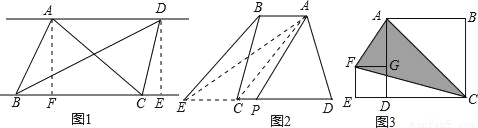
(1)自主阅读:在三角形的学习过程,我们知道三角形一边上的中线将三角形分成了两个面积相等三角形,原因是两个三角形的底边和底边上的高都相等,在此基础上我们可以继续研究:如图1,AD∥BC,连接AB,AC,BD,CD,则S△ABC=S△BCD.
证明:分别过点A和D,作AF⊥BC于F.DE⊥BC于E,由AD∥BC,可得AF=DE,又因为S△ABC=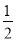 ×BC×AF,S△BCD=
×BC×AF,S△BCD=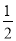 ×BC×DE .
×BC×DE .
所以S△ABC=S△BCD
由此我们可以得到以下的结论:像图1这样.
(2)问题解决:如图2,四边形ABCD中,AB∥DC,连接AC,过点B作BE∥AC,交DC延长线于点E,连接点A和DE的中点P,请你运用上面的结论证明:S?ABCD=S△APD
(3)应用拓展:
如图3,按此方式将大小不同的两个正方形放在一起,连接AF,CF,若大正方形的面积是80cm2,则图中阴影三角形的面积是 cm2.
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市2017-2018学年七年级12月月考数学试卷 题型:单选题
如图 C、D 是线段AB上的两点,且D是线段AC的中点,若AB=11,DB=8,则CB 的长为( )
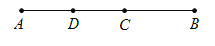
A. 3 B. 4 C. 5 D .6
C 【解析】【解析】 ∵AB=11,DB=8,∴AD=3,∵D是线段AC的中点,∴DC=AD=3,∴CB=AB-2AD=11-6=5.故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com