
(2015秋•新泰市期末)如图,在△ABC中,∠A=50°,AD为∠A的平分线,DE⊥AB,DF⊥AC,则∠DEF=( )
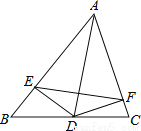
A.15° B.25° C.35° D.20°
B 【解析】 试题分析:根据角平分线性质得出DE=DF,求出∠AAED=∠AFD=90°,求出∠EDF,根据等腰三角形性质和三角形的内角和定理求出即可. 【解析】 ∵AD为∠A的平分线,DE⊥AB,DF⊥AC, ∴∠AED=∠AFD=90°,DE=DF, ∵∠EDF=360°﹣∠AED﹣∠AFD﹣∠BAC=360°﹣90°﹣90°﹣50°=130°, ∵DE=... 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:人教版八年级下册数学全册综合测试卷 题型:单选题
矩形具有而平行四边形不一定具有的性质是( )
A. 对角相等 B. 对边相等
C. 对角线相等 D. 对角线互相平分
C 【解析】试题解析:矩形的 对角线相等,而平行四边形的对角线不一定相等. 故选C.查看答案和解析>>
科目:初中数学 来源:人教版七年级下册 第1-3章 综合测试卷 题型:单选题
下列图形中,能由∠1+∠2=180°得到AB∥CD的是( )
A. 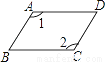 B.
B. 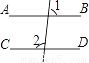
C. 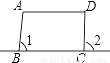 D.
D. 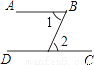
查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:填空题
请从4a2,(x+y)2,1,9b2中,任选两式做差得到的一个式子进行因式分解是________
4a2﹣1=(2a﹣1)(2a+1) 【解析】根据平方差公式,得, 4a2-1=(2a)2-12=(2a-1)(2a+1), 故答案为:4a2-1=(2a-1)(2a+1).答案不唯一.查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:单选题
如图所示,已知AB∥CD,∠A=50°,∠C=∠E.则∠C等于( )
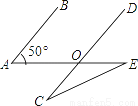
A. 20° B. 25° C. 30° D. 40°
B 【解析】∵AB∥CD,∠A=50°, ∴∠1=∠A=50°, ∵∠C=∠E,∠1=∠C+∠E, ∴∠C=1/2∠1=1/2×50°=25°. 故答案为:B.查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:单选题
下列各式中,在实数范围内能分解因式的是( )
A. x2+5 B. x2﹣5 C. x2+9 D. x2+x+1.
B 【解析】∵x 2 +5,x 2 +9,x 2 +x+1均是最简因式, ∴不能进行因式分解,故A、C、D错误; x 2 -5=(x+ )(x- ),故B正确, 故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.2 实际问题与反比例函数(第2课时) 题型:解答题
在某一电路中,保持电压不变,电流 I(安培)和电阻 R(欧姆)成反比例,当电阻 R=5欧姆时,电流 I=2安培.
(1)求 I与 R之间的函数关系式;
(2)当电流 I=0.5时,求电阻 R的值;
(3)若电阻的最大值为欧姆20,请你写出电流的范围.
(1) I= ;(2) R=20;(3)电流的范围是大于等于0.5安培. 【解析】试题分析: (1)由题意可设,代入 R=5,I=2即可求得的值,从而可得I与 R之间的函数关系式; (2)将I=0.5代入(1)中所得函数关系式即可求得对应的R的值; (3)将电阻R最大=20代入(1)中所得函数关系式即可求得对应的的电流I的最小值,由此即可电流I的取值范围. 试题解析:...查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:填空题
如图所示,Rt△AOB中,∠AOB=90°,OA=4,OB=2,点B在反比例函数y= 图象上,则图中过点A的双曲线解析式是_____.
图象上,则图中过点A的双曲线解析式是_____.
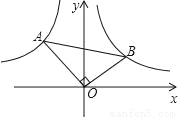
查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:解答题
网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.
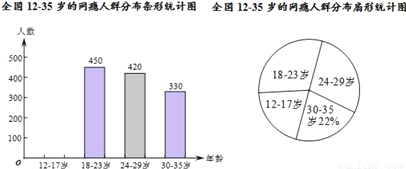
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数
(1)a=300;(2)108°;(3)12~23岁的人数为400万 【解析】试题分析:(1)根据30-35岁的人数和所占的百分比求调查的人数; (2)从调查的总人数中减去已知的三组的人数,即可得到12-17岁的人数,据此补全条形统计图; (3)先计算18-23岁的人数占调查总人数的百分比,再计算这一组所对应的圆心角的度数; (4)先计算调查中12﹣23岁的人数所占的百分比...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com