
��ijһ��·�У����ֵ�ѹ���䣬���� I(����)�͵��� R(ŷķ)�ɷ������������� R��5ŷķʱ������ I��2���࣮
(1)�� I�� R֮��ĺ�����ϵʽ��
(2)������ I��0.5ʱ������� R��ֵ��
(3)����������ֵΪŷķ20������д�������ķ�Χ��
��1�� I�� ����2�� R��20����3�������ķ�Χ�Ǵ��ڵ���0.5����. ����������������� ��1����������裬���� R��5��I��2������õ�ֵ���Ӷ��ɵ�I�� R֮��ĺ�����ϵʽ�� ��2����I��0.5���루1�������ú�����ϵʽ������ö�Ӧ��R��ֵ�� ��3��������R���=20���루1�������ú�����ϵʽ������ö�Ӧ�ĵĵ���I����Сֵ���ɴ˼��ɵ���I��ȡֵ��Χ. ���������...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���˽̰� 2018�괺 ���꼶��ѧ�²� ������ �ཻ����ƽ���� ����֤���� ���ͣ������
̽���⣺
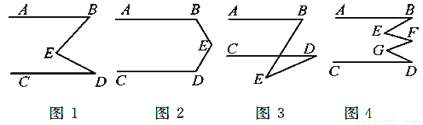
(1)��ͼ1,��AB��CD,���B+��D=��E,����˵��������
(2)������E����ͼ2��λ��,��ʱ��B����D����E֮����ʲô��ϵ��
(3)������E����ͼ3��λ��,��ʱ��B����D����E֮��Ĺ�ϵ����Σ�
(4)��ͼ4��,AB��CD,��E+��G���B+��F+��D֮���кι�ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶�²���ѧȫ���ۺϲ��Ծ� ���ͣ������
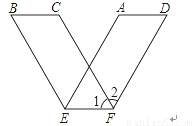
��ƽ���ı���ֽ���ضԱ�AB��CD�ϵĵ�E��F���ڵ�ֱ���۳�V����ͼ������֪ͼ�С�1=62�㣬���2�Ķ�����________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶�²���ѧȫ���ۺϲ��Ծ� ���ͣ���ѡ��
��2015��•��̩����ĩ����ͼ���ڡ�ABC�У���A=50�㣬ADΪ��A��ƽ���ߣ�DE��AB��DF��AC�����DEF=�� ��
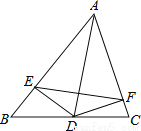
A��15�� B��25�� C��35�� D��20��
B �������� ������������ݽ�ƽ�������ʵó�DE=DF�������AAED=��AFD=90�㣬�����EDF�����ݵ������������ʺ������ε��ڽǺͶ���������ɣ� �������� ��ADΪ��A��ƽ���ߣ�DE��AB��DF��AC�� ���AED=��AFD=90�㣬DE=DF�� �ߡ�EDF=360�㩁��AED����AFD����BAC=360�㩁90�㩁90�㩁50��=130�㣬 ��DE=...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����˽̰���꼶��ѧ�²��26 ��ͬ����ʱ��ϰ��26.2 ʵ�������뷴������������2��ʱ�� ���ͣ������
һ���������һ�ݵش���ˮ20�� 3���������ˮȫ�������� t���ӣ���ˮ��Ϊ a�� 3/�֣�����ˮʱ��Ϊ5��10����
��1����д�� t�� a�ĺ�����ϵʽ����ָ�� a��ȡֵ��Χ��
��2���뻭������ͼ��
��3������ͼ��ش𣺵���ˮ��Ϊ3�� 3/��ʱ����ˮ��ʱ����Ҫ���
(1) ��(2)�����������3�� . ����������������� ��1���ɡ���ˮʱ��=��ˮ������ˮ�ٶȡ��������t�� a�ĺ�����ϵʽ�������ˮʱ��Ϊ5��10���Ӽ������a��ȡֵ��Χ�� ��2����ϣ�1������������ϵʽ��a��ȡֵ��Χ����ͼ�ɣ� ��3�����ݣ�2��������ͼ���ϣ�1�������ú�����ϵʽ���ɵõ�����ʱ��. ��������� ��1��������ɵã��� �ߵ�ʱ������ʱ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ2017-2018ѧ��Ⱦ��꼶���ϣ���ѧ��һ���¿��Ծ���11�·ݣ�(������) ���ͣ������
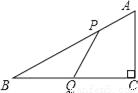
��ͼ���ڡ�ABC�У���C=90�㣬AB=10��BC=8��P��Q�ֱ���AB��BC���ϵĵ㣬��AP=BQ=a ������0��a��8����
��1����PQ��BC����a��ֵ��
��2����PQ=BQ�����߶�CQ���ŵ�Q��ת180�㣬���б��C�Ķ�Ӧ��C���Ƿ������߶�QB�ϣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ2017-2018ѧ��Ⱦ��꼶���ϣ���ѧ��һ���¿��Ծ���11�·ݣ�(������) ���ͣ������
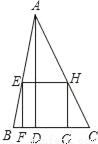
��ͼ����ABC���ڽ�������EFGH�У�EH��BC������BC=4����AD=6���������εı߳�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ2017-2018ѧ��Ⱦ��꼶���ϣ���ѧ��һ���¿��Ծ���11�·ݣ�(������) ���ͣ���ѡ��
��ͼ����ABC�У�D��E��BC���ϵĵ㣬BD��DE��EC=3��2��1��M��AC���ϣ�CM��MA=1��2��BM��AD��AE��H��G����BH��HG��GM���ڣ� ��
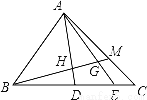
A. 4��2��1 B. 5��3��1 C. 25��12��5 D. 51��24��10
D ������������EM�� ��CE��CD=CM��CA=1��3 ��EMƽ����AD ���BHD�ס�BME����CEM�ס�CDA ��HD��ME=BD��BE=3��5��ME��AD=CM��AC=1��3 ��AH=��3����ME�� ��AH��ME=12��5 ��HG��GM=AH��EM=12��5 ��GM=5k��GH=12k�� ��BH��HM=3��2=BH��17k ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ͼ����ֱ������ϵ�У���A��Բ��A������Ϊ����1��0�����뾶Ϊ1����PΪֱ��y=��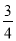 x+3�ϵĶ��㣬����P����A�����ߣ��е�ΪQ�������߳�PQ����Сֵ�ǣ� ��
x+3�ϵĶ��㣬����P����A�����ߣ��е�ΪQ�������߳�PQ����Сֵ�ǣ� ��
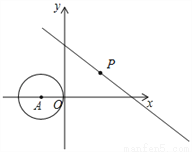
A. 3 B. 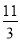 C.
C. 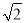 D. 2
D. 2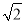
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com