
网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.
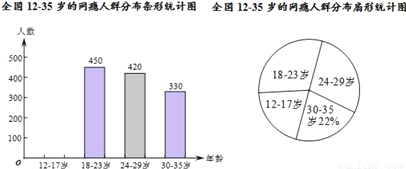
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数
(1)a=300;(2)108°;(3)12~23岁的人数为400万 【解析】试题分析:(1)根据30-35岁的人数和所占的百分比求调查的人数; (2)从调查的总人数中减去已知的三组的人数,即可得到12-17岁的人数,据此补全条形统计图; (3)先计算18-23岁的人数占调查总人数的百分比,再计算这一组所对应的圆心角的度数; (4)先计算调查中12﹣23岁的人数所占的百分比... 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:单选题
(2015秋•新泰市期末)如图,在△ABC中,∠A=50°,AD为∠A的平分线,DE⊥AB,DF⊥AC,则∠DEF=( )
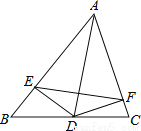
A.15° B.25° C.35° D.20°
B 【解析】 试题分析:根据角平分线性质得出DE=DF,求出∠AAED=∠AFD=90°,求出∠EDF,根据等腰三角形性质和三角形的内角和定理求出即可. 【解析】 ∵AD为∠A的平分线,DE⊥AB,DF⊥AC, ∴∠AED=∠AFD=90°,DE=DF, ∵∠EDF=360°﹣∠AED﹣∠AFD﹣∠BAC=360°﹣90°﹣90°﹣50°=130°, ∵DE=...查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:单选题
如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )
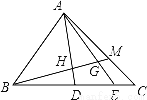
A. 4:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
D 【解析】连接EM, ∵CE:CD=CM:CA=1:3 ∴EM平行于AD ∴△BHD∽△BME,△CEM∽△CDA ∴HD:ME=BD:BE=3:5,ME:AD=CM:AC=1:3 ∴AH=(3﹣)ME, ∴AH:ME=12:5 ∴HG:GM=AH:EM=12:5 设GM=5k,GH=12k, ∵BH:HM=3:2=BH:17k ...查看答案和解析>>
科目:初中数学 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:单选题
下列命题中,错误的是( )
A. 平行四边形的对角线互相平分
B. 菱形的对角线互相垂直平分
C. 矩形的对角线相等且互相垂直平分
D. 角平分线上的点到角两边的距离相等
C 【解析】试题分析:根据平行四边形的性质对A进行判断;根据菱形的性质对B进行判断;根据矩形的性质对C进行判断;根据角平分线的性质对D进行判断. 【解析】 A、平行四边形的对角线互相平分,所以A选项的说法正确; B、菱形的对角线互相垂直平分,所以B选项的说法正确; C、矩形的对角线相等且互相平分,所以C选项的说法错误; D、角平分线上的点到角两边的距离相等,所以D选...查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:解答题
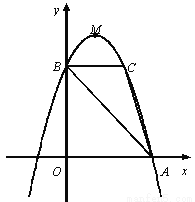
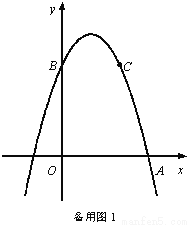
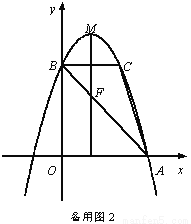
如图,抛物线y=ax 2+bx+c的顶点为M(1,4),与x轴的右交点为A,与y轴的交点为B,点C与点B关于抛物线的对称轴对称,且S△ABC =3.
(1)求抛物线的解析式;
(2)点D是y轴上一点,将点D绕C点逆时针旋转90°得到点E,若点E恰好落在抛物线上,请直接写出点D的坐标;
(3)设抛物线的对称轴与直线AB交于点F,问:在x轴上是否存在点P,使得以P、A、F为顶点的三角形与△ABC相似?若存在,求点P的坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:填空题
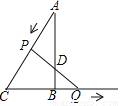
如图,在△ABC中∠ABC=90°,,AB=4 cm, BC=3cm,动点P以3cm/s的速度由A向C运动,动点Q同时以1cm/s的速度由B向CB的延长线方向运动,连PQ交AB于D,则当运动时间为____s时,△ADP是以AP为腰的等腰三角形.
查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:单选题
如图,在直角坐标系中,⊙A的圆心A的坐标为(﹣1,0),半径为1,点P为直线y=﹣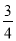 x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是( )
x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是( )
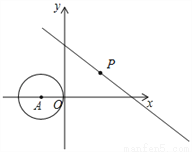
A. 3 B. 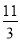 C.
C. 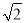 D. 2
D. 2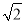
查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学 第三章 图形的平移与旋转 单元检测卷 题型:填空题
如图所示,该图形是________ 对称图形.
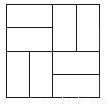
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册数学 第六章 概率初步 单元检测卷 题型:解答题
王勇和李明两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了30次实验,实验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 2 | 5 | 6 | 4 | 10 | 3 |
(1)分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率;
(2)王勇说:“根据以上实验可以得出结论:由于5点朝上的频率最大,所以一次实验中出现5点朝上的概率最大”;李明说:“如果投掷300次,那么出现6点朝上的次数正好是30次”.试分别说明王勇和李明的说法正确吗?并简述理由;
(3)现王勇和李明各投掷一枚骰子,请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
(1); (2)王勇的说法是错误的,李明的说法也是错误的(3) 【解析】试题分析:(1)、根据概率的计算法则分别求出“3点朝上”和“5点朝上”的概率;(2)、根据随机事件的性质来分别进行说明;(3)、首先将所得的所有结果用列表法来表示出来,然后找出符合条件的情况,最后根据概率的计算法则求出答案. 试题解析:(1)“3点朝上”的频率为:, “5点朝上”的频率为:; (2)王勇...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com